
假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
| x | 2 | 3 | 4 | 5 | 6 |
| y | 1.4 | 2.3 | 3.1 | 3.7 | 4.5 |
若由资料可知y对x呈线性相关关系,且线性回归方程为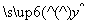 =a+bx,其中已知b=1.23,请估计使用年限为20年时,维修费用约为________.
=a+bx,其中已知b=1.23,请估计使用年限为20年时,维修费用约为________.
科目:高中数学 来源: 题型:
若对于预报变量y与解释变量x的10组统计数据的回归模型中,计算R2=0.95,又知残差平方和为120.55,那么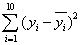 的值为
的值为
A.241.1 B.245.1 C.2411 D.2451
查看答案和解析>>
科目:高中数学 来源: 题型:
若α、β的终边关于y轴对称,则下列等式正确的是( )
A.sinα=sinβ B.cosα=cosβ C.tanα=tanβ D.tanα·tanβ=1
查看答案和解析>>
科目:高中数学 来源: 题型:
下列四个结论:
⑴两条不同的直线都和同一个平面平行,则这两条直线平行.
⑵两条不同的直线没有公共点,则这两条直线平行.
⑶两条不同直线都和第三条直线垂直,则这两条直线平行.
⑷一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行.
其中正确的个数为 ( )
A. B.
B.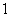 C.
C. D.
D.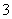
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2cos2x+2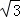 sinxcosx+1.
sinxcosx+1.
(Ⅰ)求函数f(x)的单调递增区间,最小正周期;
(Ⅱ)画出f(x)的图象.(要求:列表,要有超过一个周期的图象,并标注关键点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com