
分析 (Ⅰ)由题意利用两个向量的数量积的定义求得$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值.
(Ⅱ)根据($\overrightarrow{a}$+λ$\overrightarrow{b}$)•$\overrightarrow{a}$=0,求得λ的值.
解答 解:(Ⅰ)由题意可得$\left|{a}\right|=\sqrt{{{(-3)}^2}+{4^2}}=5$,$\left|{b}\right|=\sqrt{{2^2}+{2^2}}=2\sqrt{2}$,$\overrightarrow{a}•\overrightarrow{b}$=x1x2+y1y2=-6+8=2,
∴$cosθ=\frac{{{a}•{b}}}{{\left|{a}\right|\left|{b}\right|}}=\frac{1}{{5\sqrt{2}}}=\frac{{\sqrt{2}}}{10}$,即 $\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值为$\frac{\sqrt{2}}{10}$.
(Ⅱ)$\overrightarrow{a}$+λ$\overrightarrow{b}$=(-3+2λ,4+2λ),∵$\overrightarrow{a}$+λ$\overrightarrow{b}$与$\overrightarrow{a}$垂直,
则($\overrightarrow{a}$+λ$\overrightarrow{b}$)•$\overrightarrow{a}$=(-3)(-3+2λ)+4(4+2λ)=0,解得$λ=-\frac{25}{2}$.
点评 本题主要考查两个向量垂直的条件,两个向量坐标形式的运算,属于基础题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
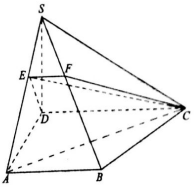 如图,在直角梯形ABCD中,∠ADC=∠BAD=90°,AB=AD=1,CD=2,平面SAD⊥平面ABCD,平面SDC⊥平面ABCD,SD=$\sqrt{3}$,在线段SA上取一点E(不含端点)使EC=AC,截面CDE交SB于点F.
如图,在直角梯形ABCD中,∠ADC=∠BAD=90°,AB=AD=1,CD=2,平面SAD⊥平面ABCD,平面SDC⊥平面ABCD,SD=$\sqrt{3}$,在线段SA上取一点E(不含端点)使EC=AC,截面CDE交SB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,-$\frac{11}{2}$) | B. | ($\frac{1}{2}$,-$\frac{11}{4}$) | C. | (2,-$\frac{11}{2}$) | D. | ($\frac{1}{2}$,-$\frac{7}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤3} | B. | {x|2<x<3} | C. | {x|-1≤x≤3} | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
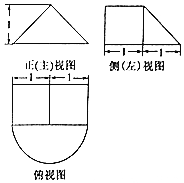 一个由半圆锥和平放的直三棱柱(侧棱垂直于底面的三棱柱)组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半圆锥和平放的直三棱柱(侧棱垂直于底面的三棱柱)组成的几何体,其三视图如图所示,则该几何体的体积为( )| A. | 1+$\frac{π}{3}$ | B. | 1+$\frac{π}{6}$ | C. | $\frac{2}{3}$+$\frac{π}{3}$ | D. | $\frac{2}{3}$+$\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com