练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设＝(2cosx，1)，＝(cosx，sin2x)，f(x)＝·，xR．

    (1)若f(x)＝0且x[－，]，求x的值．

    (2)若函数g(x)＝cos(w x－)＋k(w ＞0，k∈R)与f(x)的最小正周期相同，且g(x)的图象过点(，2)，求函数g(x)的值域及单调递增区间．

    答案：
    解析：

    　　解：(Ⅰ)f(x)＝·＝2cos2x＋sin2x

    　　＝1＋cos2x＋sin2x＝2sin(2x＋)＋1　　3分

    　　f(x)＝0，2sin(2x＋)＋1＝0，sin(2x＋)＝－　　4分

    　　又x[－，]　－　　5分

    　　　x＝－　　6分

    　　(Ⅱ)由(Ⅰ)知，f(x)＝2sin(2x＋)＋1，

    　　因为g(x)与f(x)的最小正周期相同＝2　　7分

    　　又g(x)的图象过点(，2)，cos(2×－)＋k＝2，1＋k＝2，k＝1　　8分

    　　g(x)＝cos(2x－)＋1，其值域为[0，2]　　9分

    　　2k－2x－2k，kZ　　10分

    　　k－xk＋，kZ　　11分

    　　所以函数的单调增区间为[k－，k＋]，kZ　　12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：浙江省杭州高中2006-2007学年度第一学期高三年级第三次月考　数学试题(理) 题型：044

    解答题：解答应写出文字说明，证明过程或演算步骤．

    设函数f(x)＝a·b，其中向量a＝(2cosx，1)，向量b＝(cosx，－sin2x)，x∈R．

    (1)

    求函数f(x)的单调减区间

    (2)

    若，求函数f(x)的值域

    (3)

    若函数y＝f(x)的图象按向量c＝(m，n)(|m|＜＝平移后得到函数y＝2sin2x的图象，求实数m，n的值．

    查看答案和解析>>

    科目：高中数学 来源：浙江省杭州高中2006-2007学年度第一学期高三年级第三次月考　数学试题(文) 题型：044

    解答题：解答应写出文字说明，证明过程或演算步骤．

    设函数f(x)＝a·b，其中向量a＝(2cosx，1)，b＝(cosx－sin2x)，x∈R

    (1)

    求函数f(x)的单调减区间

    (2)

    若，求函数f(x)的值域

    (3)

    若函数y＝f(x)的图象按向量c＝(m，n)(|m|＜＝平移后得到函数y＝2sin2x的图象，求实数m，n的值．

    查看答案和解析>>

    科目：高中数学 来源：福建省福州八县(市)一中2012届高三上学期期中联考数学文科试题 题型：044

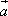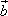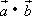    设＝(2cosx，1)，＝(cosx，sin2x)，f(x)＝，x∈R．

    (1)若f(x)＝0且x∈[0，]，求x的值；

    (2)若函数g(x)＝(ω＞0，k∈R)与f(x)的最小正周期相同，且g(x)的图象过点(，2)，求函数g(x)的值域及单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (本小题满分12分)

    设＝(2cosx,1),＝(cosx,sin2x),f(x)＝·，xR.

    ⑴ 若f(x)＝0且x[－,],求x的值.

    ⑵ 若函数g(x)＝cos(wx－)＋k(w＞0, kR)与f(x)的最小正周期相同，且g(x)的图象过点(，2)，求函数g(x)的值域及单调递增区间.

    查看答案和解析>>

    同步练习册答案