
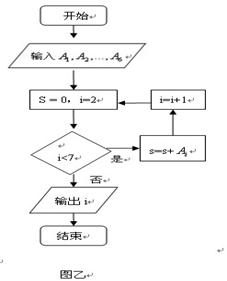
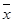 ,将10场比赛得分
,将10场比赛得分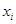 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的 大小为多少?并说明
大小为多少?并说明 的统计学意义;
的统计学意义;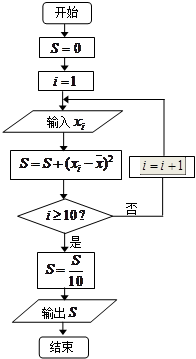
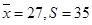 ,意义见解析。(Ⅲ)
,意义见解析。(Ⅲ)
 ,
, 表示甲运动员的得分,
表示甲运动员的得分, 表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件有20种,其中甲的得分大于乙的得分有4种,利用概率公式解得。
表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件有20种,其中甲的得分大于乙的得分有4种,利用概率公式解得。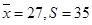 .………………………………………………6分
.………………………………………………6分 表示10场比赛得分的方差,是描述比赛得分离散程度的量,
表示10场比赛得分的方差,是描述比赛得分离散程度的量, 值越小,表示比赛得分比较集中,
值越小,表示比赛得分比较集中, 值
值 ,
, 表示甲运动员的得分,
表示甲运动员的得分, 表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件为:
表示乙运动员的得分,则甲、乙两位运动员的10场得分中各随机抽取一场不小于30分的得分的基本事件为: ,
, ,
, ,
, ,
, ;
;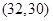 ,
, ,
, ,
, ,
, ;
; ,
, ,
, ,
, ,
, ;
;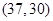 ,
, ,
, ,
, ,
, ;共有20种情况,…10分。
;共有20种情况,…10分。 ,
,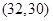 ,
, ,
,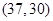 ,共4种情况.………11分
,共4种情况.………11分 .………………………………12分
.………………………………12分

科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,
,
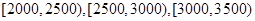 ,
,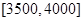 的人数依次为
的人数依次为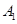 、
、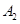 、……、
、……、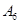 .图乙是统计图甲中月工资收
.图乙是统计图甲中月工资收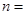 ;图乙
;图乙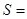 .(用数字作答)
.(用数字作答)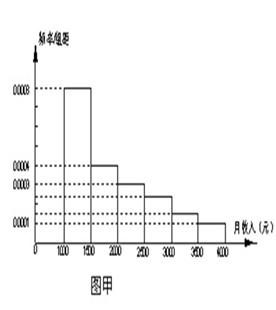
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 (含80)以上时,属醉酒驾车。属醉酒驾车。据有关调查,在一周内,某地区查处酒后驾车和醉酒驾车共100
(含80)以上时,属醉酒驾车。属醉酒驾车。据有关调查,在一周内,某地区查处酒后驾车和醉酒驾车共100
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ;
; ;
;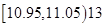 ;
; ;
; ;
; ;
; ;
;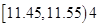 ;
; ;
; 范围内的可能性是百分之几?
范围内的可能性是百分之几?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com