
(10分)已知函数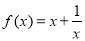
(Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅱ)用定义证明 在
在 上是减函数;
上是减函数;
(Ⅲ)函数 在
在 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
(Ⅰ)函数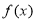 为奇函数;(Ⅱ) 略;(Ⅲ)
为奇函数;(Ⅱ) 略;(Ⅲ) 在(﹣1,0)上是减函数.
在(﹣1,0)上是减函数.
【解析】
试题分析:(Ⅰ) 首先求函数 定义域并验证其定义域是否关于原点对称,再根据奇函数的定义验证
定义域并验证其定义域是否关于原点对称,再根据奇函数的定义验证 即证;(Ⅱ) 根据减函数的定义,证明当
即证;(Ⅱ) 根据减函数的定义,证明当 且
且 时,总有
时,总有 即证;(Ⅲ) 由(Ⅰ)可知函数
即证;(Ⅲ) 由(Ⅰ)可知函数 为奇函数,其图像关于原点对称,得
为奇函数,其图像关于原点对称,得 在(﹣1,0)上是减函数。
在(﹣1,0)上是减函数。
试题解析:(Ⅰ)函数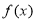 为奇函数,理由如下:
为奇函数,理由如下:
易知函数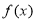 的定义域为:
的定义域为: ,关于坐标原点对称.
,关于坐标原点对称.
又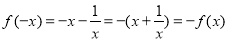

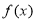 在定义域上是奇函数.
在定义域上是奇函数.
(Ⅱ)设 且
且 ,则
,则

∵0<x1<x2<1,∴x1x2<1,x1x2﹣1<0,
又∵x2>x1∴x2﹣x1>0.
∴ ,即
,即
因此函数 在(0,1)上是减函数.
在(0,1)上是减函数.
(Ⅲ) 在(﹣1,0)上是减函数.
在(﹣1,0)上是减函数.
考点:1、奇、偶函数的判定方法;2、函数单调性的判定方法;3、函数的单调区间.


科目:高中数学 来源:2014-2015学年浙江省嘉兴市高二上学期第一次阶段测试数学试卷(解析版) 题型:选择题
若a<0,-1<b<0,则a,ab,ab2之间的大小关系是
A.a>ab>ab2 B.ab2>ab>a C.ab>a>ab2 D.ab>ab2>a
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南郑州外国语学校高二上学期第一次月考理科数学卷(解析版) 题型:选择题
在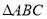 中,若
中,若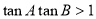 ,则
,则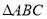 是( )
是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南郑州外国语学校高二上学期第一次月考文科数学卷(解析版) 题型:选择题
已知数列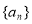 为等差数列,若
为等差数列,若 且它们的前
且它们的前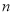 项和
项和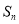 有最大值,则使得
有最大值,则使得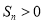 的
的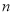 的最大值为( )
的最大值为( )
A.16 B.17 C.18 D.19
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南郑州外国语学校高二上学期第一次月考文科数学卷(解析版) 题型:选择题
在△ABC中,若 ,
, ,
, ,则角
,则角 的大小为( )
的大小为( )
A.  B.
B. C.
C. 或
或 D.
D. 或
或 
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省郑州市高二10月月考数学试卷(解析版) 题型:选择题
从标有1,2,3,4的卡片中先后抽出两张卡片,则号码4“在第一次被抽到的概率”、“在第一次未被抽到而第二次被抽到的概率”、“在整个抽样过程中被抽到的概率”分别是( )
A、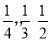 B、
B、 C、
C、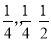 D、
D、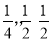
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com