D
分析:由题设,可对x
n=f(x
n-1)(n=2,3,4,…),进行变形,得到x
n-1+4=
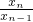
,由此关系对任意的n=2,3,4,…,都成立,由此得到x
n-2+4=

,…,x
1+4=

,各式相乘得出x
1的表达式,再由题设中数列{x
n}中的项能取的不同的值为有限个判断出x
1的不同的值的个数m.
解答:由题意(x
n-1)
2+4(x
n-1)=x
n,即(x
n-1+4)×(x
n-1)=x
n,即x
n-1+4=
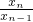
,
故有x
n-2+4=

,…,x
1+4=

各式相乘得:(x
1+4)(x
2+4)(x
3+4)(x
4+4)…(x
n-1+4)=
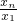
∴x
1=

x
n能取得的值为有限的,而被除的部分(x
1+4)(x
2+4)(x
3+4)(x
4+4)…(x
n-1+4)的值随着n的变化面变化,知x
1的不同取值有无穷个,故m的取值为无穷个
故选D
点评:本题考查数列与函数的综合,解题的关键是根据所给的数列的递推关系,构造出x
1的表达式,再由所得的形式判断出它的取值的个数,本题比较抽象,较难理解,此类题易因为不理解而导致无法下手,千百万解题失败,题后要注意总结本题的做题规律及问题转化的依据,本题在变形过程中用到了累乘的技巧,积累一些变形技巧对解题很有帮助.

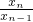 ,由此关系对任意的n=2,3,4,…,都成立,由此得到xn-2+4=
,由此关系对任意的n=2,3,4,…,都成立,由此得到xn-2+4= ,…,x1+4=
,…,x1+4= ,各式相乘得出x1的表达式,再由题设中数列{xn}中的项能取的不同的值为有限个判断出x1的不同的值的个数m.
,各式相乘得出x1的表达式,再由题设中数列{xn}中的项能取的不同的值为有限个判断出x1的不同的值的个数m.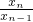 ,
, ,…,x1+4=
,…,x1+4=