
 .
.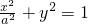 (a>0),则离心率为
(a>0),则离心率为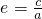 =
=
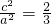 ,而b2=1,解得a2=3,…(4分)
,而b2=1,解得a2=3,…(4分) .…(5分)
.…(5分)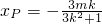 ,从而yP=kxP+m=
,从而yP=kxP+m=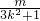 ,
,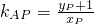 =-
=- (m=0不满足题目条件)
(m=0不满足题目条件) =-
=- ,即2m=3k2+1,②…(9分)
,即2m=3k2+1,②…(9分)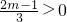 ,解得m>
,解得m> .
.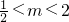 …(11分)
…(11分) ,即可确定椭圆的几何量,从而可求椭圆的方程;
,即可确定椭圆的几何量,从而可求椭圆的方程;

科目:高中数学 来源: 题型:解答题
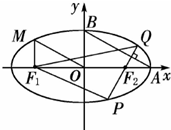 (普通班)如图所示,从椭圆
(普通班)如图所示,从椭圆 上一点M向x轴作垂线,恰好通过椭
上一点M向x轴作垂线,恰好通过椭查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 )+2|sin(π+x)|(x∈[0,2π])的图象与直线y=k有且仅有两个不同交点,则k的取值范围是
)+2|sin(π+x)|(x∈[0,2π])的图象与直线y=k有且仅有两个不同交点,则k的取值范围是查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com