
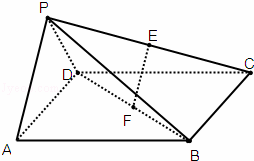
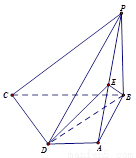
如图在四棱锥P﹣ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=![]() AD,设E、F分别为PC、BD的中点.
AD,设E、F分别为PC、BD的中点.
(Ⅰ) 求证:EF∥平面PAD;
(Ⅱ) 求证:面PAB⊥平面PDC;
(Ⅲ) 求二面角B﹣PD﹣C的正切值.
| 考点: | 用空间向量求平面间的夹角;直线与平面平行的判定;平面与平面垂直的判定. |
| 专题: | 证明题;空间位置关系与距离. |
| 分析: | (Ⅰ)利用线面平行的判定定理:连接AC,只需证明EF∥PA,利用中位线定理即可得证; (Ⅱ)利用面面垂直的判定定理:只需证明PA⊥面PDC,进而转化为证明PA⊥PD,PA⊥DC,易证三角形PAD为等腰直角三角形,可得PA⊥PD;由面PAD⊥面ABCD的性质及正方形ABCD的性质可证CD⊥面PAD,得CD⊥PA; (Ⅲ)设PD的中点为M,连结EM,MF,则EM⊥PD,由(Ⅱ)可证PD⊥平面EFM,则∠EMF是二面角B﹣PD﹣C的平面角,通过解Rt△FEM可得所求二面角的正切值; |
| 解答: | (Ⅰ)证明:ABCD为平行四边形, 连结AC∩BD=F,F为AC中点,E为PC中点, ∴在△CPA中EF∥PA,且PA⊂平面PAD,EF⊄平面PAD, ∴EF∥平面PAD; (Ⅱ)证明:因为面PAD⊥面ABCD,平面PAD∩面ABCD=AD,ABCD为正方形, ∴CD⊥AD,CD⊂平面ABCD, 所以CD⊥平面PAD,∴CD⊥PA, 又 所以△PAD是等腰直角三角形,且 CD∩PD=D,且CD、PD⊂面ABCD,PA⊥面PDC, 又PA⊂面PAB, ∴面PAB⊥面PDC; (Ⅲ)解:设PD的中点为M,连结EM,MF,则EM⊥PD, 由(Ⅱ)知EF⊥面PDC,EF⊥PD,PD⊥面EFM,PD⊥MF,∠EMF是二面角B﹣PD﹣C的平面角, Rt△FEM中, 故所求二面角的正切值为
|
| 点评: | 本题考查线面平行、面面垂直的判定及二面角的求解,考查学生的推理论证能力及逻辑思维能力,属中档题. |


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
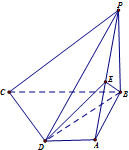 如图,四棱锥P--ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
如图,四棱锥P--ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.查看答案和解析>>
科目:高中数学 来源: 题型:
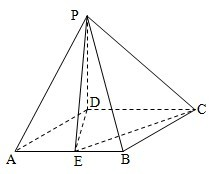 如图,四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是边长为2的菱形,∠BAD=
如图,四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是边长为2的菱形,∠BAD=| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (理)如图,四棱锥P-ABCD的底面是矩形,PA⊥面ABCD,PA=2
(理)如图,四棱锥P-ABCD的底面是矩形,PA⊥面ABCD,PA=2| 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:
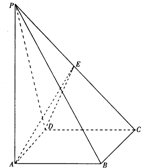 如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,AB=1,PA=
如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,AB=1,PA=| 6 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省元月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,四棱锥P--ABCD中,PB 底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
(1)求异面直线PA与CD所成的角;
(2)求证:PC∥平面EBD;
(3)求二面角A—BE--D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com