
| 3 | 64 |
|


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:013
选择题:
(1)
已知 ,
, ,
, ,则
,则
[
]|
(A)A 、B、D三点共线 |
(B)A 、B、C三点共线 |
|
(C)B 、C、D三点共线 |
(D)A 、C、D三点共线 |
(2)
已知正方形ABCD的边长为1, ,
, ,
, ,则
,则 等于
等于
[
]|
(A)0 |
(B)3 |
(C) |
(D) |
(3)
已知 ,
, ,
, ,
, ,且四边形ABCD为平行四边形,则
,且四边形ABCD为平行四边形,则
[
]|
(A)a +b+c+d=0 |
(B)a -b+c-d=0 |
|
(C)a +b-c-d=0 |
(D)a -b-c+d=0 |
(4)
已知D、E、F分别是△ABC的边BC、CA、AB的中点,且 ,
, ,
, ,则①
,则① ;②
;② ;③
;③ ;④
;④
中正确的等式的个数为
[
]|
(A)1 |
(B)2 |
(C)3 |
(D)4 |
(5)
若 ,
, 是夹角为60°的两个单位向量,则
是夹角为60°的两个单位向量,则 ;
; 的夹角为
的夹角为
[
]|
(A)30° |
(B)60° |
(C)120° |
(D)150° |
(6)
若向量a、b、c两两所成的角相等,且 ,
,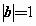 ,
, ,则
,则 等于
等于
[
]|
(A)2 |
(B)5 |
(C)2 或5 |
(D)  |
(7)
等边三角形ABC的边长为1, ,
, ,
, ,那么a·b+b·c+c·a等于
,那么a·b+b·c+c·a等于
[
]|
(A)3 |
(B) -3 |
(C) |
(D) |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知![]() ≤a≤1,若f(x)=ax2-2x+1在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)- N(a)。
≤a≤1,若f(x)=ax2-2x+1在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)- N(a)。
(1)求g(a)的解析式;
(2)当![]() ≤ a ≤ 1时,求函数g(a)的最小值。
≤ a ≤ 1时,求函数g(a)的最小值。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都七中高一(上)期中数学试卷(解析版) 题型:选择题
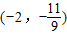
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都七中高一(上)期中数学试卷(解析版) 题型:选择题
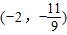
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com