Question

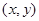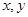袋子中有质地、大小完全相同的4个球，编号分别为1，2，3，4．甲、乙两人玩一种游戏：甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，若两个编号的和为奇数算甲赢，否则算乙赢．记基本事件为（x，y），其中x、y分别为甲、乙摸到的球的编号．
（Ⅰ）列举出所有的基本事件，并求甲赢且编号的和为5的事件发生的概率；
（Ⅱ）比较甲胜的概率与乙胜的概率，并说明这种游戏规则是否公平．

Answer 1

分析：（1）甲乙两人各摸一球，记为基本事件（x，y），这是一个有放回、有序的问题，结合球的编号分别为1，2，3，4．我们不难列出所有的基本事件，再列举出编号的和为5的事件个数，代入古典概型公式，即可求解．
（2）由两个编号的和为奇数算甲赢，否则算乙赢，我们分别统计甲赢和乙赢的基本事件个数，然后代入古典概型公式，计算出甲胜的概率与乙胜的概率，比较后即可得到结论．

解答：解：（Ⅰ）共有16个等可能性的基本事件，列举如下：
（1，1），（1，2），（1，3），（1，4），
（2，1），（2，2），（2，3），（2，4），
（3，1），（3，2），（3，3），（3，4），
（4，1），（4，2），（4，3），（4，4），（2分）
设“甲胜且两数字之和为5”为事件A，则事件A包含：
（1，4），（2，3），（3，2），（4，1）4个基本事件（4分）
∴P(A)=

4

16

=

1

4

为所求的概率．（6分）
（Ⅱ）这种游戏规则公平．
设“甲胜”为事件B，“乙胜”为事件C，
则甲胜即两数字之和为奇数所包含的基本事件数为8个：
（1，2），（1，4），（2，1），（2，3），
（3，2），（3，4），（4，1），（4，3），（8分）
∴甲胜的概率P(B)=

8

16

=

1

2

，（9分）
从而乙胜的概率P(C)=1-P(B)=1-

1

2

=

1

2

．（11分）
∴P（B）=P（C），故这种游戏规则公平．（12分）

点评：本题考查的知识点是古典概型，古典概型要求所有结果出现的可能性都相等，强调所有结果中每一结果出现的概率都相同．弄清一次试验的意义以及每个基本事件的含义是解决问题的前提，正确把握各个事件的相互关系是解决问题的关键．解决问题的步骤是：计算满足条件的基本事件个数，及基本事件的总个数，然后代入古典概型计算公式进行求解．