
分析 (Ⅰ)x2-2xy+4y2=1,变形为(x-y)2+3y2=1,换元,再利用三角函数知识,即可证明;
(Ⅱ)由y=$\frac{sinθ}{\sqrt{3}}$,θ∈(0,$\frac{π}{2}$],即可求出y的取值范围.
解答 (Ⅰ)证明:x2-2xy+4y2=1,变形为(x-y)2+3y2=1,
∵x>0,y>0,令y=$\frac{sinθ}{\sqrt{3}}$,x-y=cosθ,θ∈(0,$\frac{π}{2}$].
则x=cosθ+$\frac{sinθ}{\sqrt{3}}$.
∴x+2y=cosθ+$\sqrt{3}$sinθ=2sin(θ+$\frac{π}{6}$),
∴x+2y≤2;
(Ⅱ)解:∵y=$\frac{sinθ}{\sqrt{3}}$,θ∈(0,$\frac{π}{2}$],
∴y的取值范围是(0,$\frac{\sqrt{3}}{3}$].
点评 本题考查了三角变换、配方法、三角函数的单调性、两角和差的正弦公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或2 | B. | 2 | C. | 1 | D. | 1或-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>b,则ac>bc”是真命题 | |
| B. | 命题“若a2+b2=0,则a,b全为0”是真命题 | |
| C. | 命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0” | |
| D. | 命题“若a=0,则ab=0”的逆否命题是“若ab≠0,则a≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
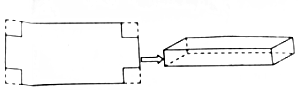 如图,在一张长为2a米,宽为a米(a>2)的矩形铁皮的四个角上,各剪去一个边长是x米(0<x≤1)的小正方形,折成一个无盖的长方体铁盒,设V(x)表示铁盒的容积.
如图,在一张长为2a米,宽为a米(a>2)的矩形铁皮的四个角上,各剪去一个边长是x米(0<x≤1)的小正方形,折成一个无盖的长方体铁盒,设V(x)表示铁盒的容积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=$\frac{π}{3}$,AD=2,DE=$\sqrt{3}$.
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=$\frac{π}{3}$,AD=2,DE=$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com