
 与双曲线
与双曲线 有公共点P,则P与双曲线二焦点连线构成三角形面积为( )
有公共点P,则P与双曲线二焦点连线构成三角形面积为( )
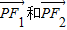 ,cos∠F1PF2,最后利用三角形面积公式计算即可.
,cos∠F1PF2,最后利用三角形面积公式计算即可.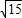 ,
,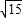 ,PF2=5-
,PF2=5-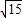 ,
,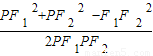 =
=
 PF1•PF2sin∠F1PF2=
PF1•PF2sin∠F1PF2= (5+
(5+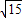 )(5-
)(5-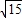 )×
)× =3
=3

科目:高中数学 来源:2011届重庆市高三高考前冲刺试卷理数 题型:单选题
.光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如题10图,椭圆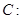
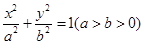 与双曲线
与双曲线 有公共焦点,现一光线从它们的左焦点出发,在椭圆与双曲线间连续反射,则光线经过
有公共焦点,现一光线从它们的左焦点出发,在椭圆与双曲线间连续反射,则光线经过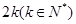 次反射后回到左焦点所经过的路径长为
次反射后回到左焦点所经过的路径长为
A. | B.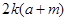 | C. | D. |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市浦东新区高三4月高考预测(二模)理科数学试卷(解析版) 题型:解答题
(1)设椭圆 :
: 与双曲线
与双曲线 :
: 有相同的焦点
有相同的焦点 ,
, 是椭圆
是椭圆 与双曲线
与双曲线 的公共点,且
的公共点,且 的周长为
的周长为 ,求椭圆
,求椭圆 的方程;
的方程;
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.
(2)如图,已知“盾圆 ”的方程为
”的方程为 .设“盾圆
.设“盾圆 ”上的任意一点
”上的任意一点 到
到 的距离为
的距离为 ,
, 到直线
到直线 的距离为
的距离为 ,求证:
,求证: 为定值;
为定值;

(3)由抛物线弧 :
: (
(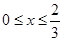 )与第(1)小题椭圆弧
)与第(1)小题椭圆弧 :
: (
( )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆 ”.设过点
”.设过点 的直线与“盾圆
的直线与“盾圆 ”交于
”交于 两点,
两点, ,
,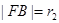 且
且 (
( ),试用
),试用 表示
表示 ;并求
;并求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆市六校联考高二(上)期末数学试卷(理科)(解析版) 题型:选择题
 与双曲线
与双曲线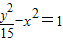 有公共点P,则P与双曲线二焦点连线构成三角形面积为( )
有公共点P,则P与双曲线二焦点连线构成三角形面积为( )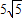
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com