
已知圆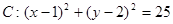 ,直线
,直线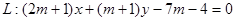
(1)求证:直线恒过定点
(2)判断直线被圆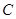 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时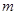 的值及最短长度。
的值及最短长度。
(1)见解析(2)当直线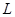 垂直于
垂直于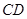 时被截得弦长最短,此时
时被截得弦长最短,此时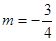 ,最短弦长为
,最短弦长为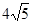
【解析】
试题分析:(1)证明:直线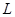 的方程
的方程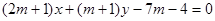 ,
,
经整理得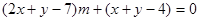 ,
……1分
,
……1分
由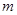 的任意性
的任意性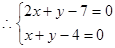 ,
……3分
,
……3分
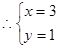
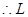 恒过定点
恒过定点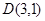 .
……5分
.
……5分
(2)解:因为直线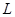 恒经过圆
恒经过圆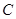 内一点
内一点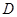 ,当直线
,当直线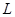 垂直于
垂直于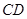 时被截得弦长最短. ……7分
时被截得弦长最短. ……7分
由 、
、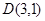 ,直线
,直线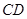 斜率
斜率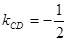 ,
,
又直线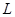 与直线
与直线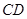 垂直,
垂直,
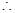 直线
直线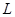 的斜率为2,
的斜率为2,
于是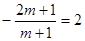 ,
,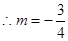 ,
……9分
,
……9分
最短弦长为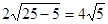 ,
……11分
,
……11分
综上所述,当直线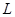 垂直于
垂直于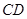 时被截得弦长最短,
时被截得弦长最短,
此时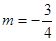 ,最短弦长为
,最短弦长为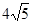 .
……12分
.
……12分
考点:本小题主要考查直线过定点、直线与圆的位置关系、弦长等问题,考查学生分析问题、解决问题的能力和运算求解能力.
点评:当直线与圆相交时,圆心到直线的距离、半弦长和半径组成一个直角三角形,这个直角三角形在解题时经常用到.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源:2012-2013学年河南扶沟高级中学高一第三次考试数学试卷(带解析) 题型:解答题
已知圆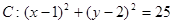 ,直线
,直线
(1)求证:直线恒过定点
(2)判断直线被圆 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时 的值及最短长度。
的值及最短长度。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省扶余一中高一上学期期末考试理科数学试(带解析)卷 题型:解答题
(本小题满分12分)已知圆C: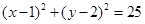 ,直线L:
,直线L: 

(1) 证明:无论 取什么实数,L与圆恒交于两点;
取什么实数,L与圆恒交于两点;
(2) 求直线被圆C截得的弦长最小时直线L的斜截式方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com