练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知EFGH－E1F1G1H1是所有棱长都相等的平行六面体，且∠E1EF＝∠E1EH＝∠EFH＝，则对角面F1FHH1一定是

    [　　]

    A．平行四边形但不是菱形

    B．矩形但不是正方形

    C．菱形但不是正方形

    D．正方形

    答案：D
    解析：

    设棱长为a

        


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

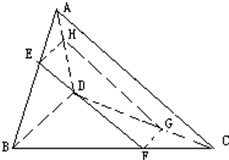    如图，要在呈空间四边形的支架上安装一块矩形的太阳能吸光板（图中EFGH），矩形的四个顶点分别在空间四边形ABCD的边上．已知AC=a，BD=b，试问：E、F、G、H分别在什么位置时，吸光板的面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知P是正方形EFGH所在平面外一点，且PE⊥面EFGH，则面PEF（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

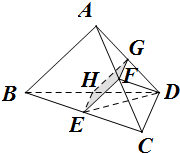    已知四面体ABCD中，DC⊥BD，AB=AD=2DC=2．AD⊥平面EFGH，且AB∥截面EFGH，CD∥截面EFGH．
    （Ⅰ）求证：GF∥CD，AB∥GH；
    （Ⅱ）求证：GF⊥平面ABD；
    （Ⅲ）设GD=x，求四棱锥D-EFGH的体积V（x）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•泉州模拟）某工厂欲加工一件艺术品，需要用到三棱锥形状的坯材，工人将如图所示的长方体ABCD-EFGH材料切割成三棱锥H-ACF．

    （Ⅰ）若点M，N，K分别是棱HA，HC，HF的中点，点G是NK上的任意一点，求证：MG∥平面ACF；
    （Ⅱ）已知原长方体材料中，AB=2m，AD=3m，DH=1m，根据艺术品加工需要，工程师必须求出该三棱锥的高．
    （i） 甲工程师先求出AH所在直线与平面ACF所成的角θ，再根据公式h=AH•sinθ求出三棱锥H-ACF的高．请你根据甲工程师的思路，求该三棱锥的高．
    （ii）乙工程师设计了一个求三棱锥的高度的程序，其框图如图所示，则运行该程序时乙工程师应输入的t的值是多少？（请直接写出t的值，不要求写出演算或推证的过程）．

    查看答案和解析>>

    同步练习册答案