
分析 根据向量的数量积公式以及向量的垂直的条件即可求出.
解答 解:|$\vec a$|=3$\sqrt{2}$,|$\vec b$|=4,<${\vec a$,$\vec b}$>=135°,
∴$\overrightarrow{a}•\overrightarrow{b}$=|$\vec a$|•|$\vec b$|cos135°=3$\sqrt{2}$×4×(-$\frac{\sqrt{2}}{2}$)=-12,
∵$\vec m$⊥$\vec n$,$\vec m$=$\vec a$+$\vec b$,$\vec n$=$\vec a$+λ$\vec b$,
∴$\overrightarrow{m}$•$\overrightarrow{n}$=($\vec a$+$\vec b$)($\vec a$+λ$\vec b$)=|$\vec a$|2+λ|$\vec b$|2+(1+λ)$\overrightarrow{a}•\overrightarrow{b}$=18+16λ-12(1+λ)=0,
解得λ=$-\frac{3}{2}$,
故答案为:$-\frac{3}{2}$
点评 本题考查了向量的数量积公式以及向量的垂直的条件,属于基础题.


科目:高中数学 来源: 题型:解答题
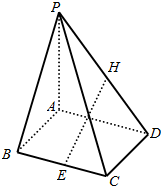 如图,已知四棱锥P-ABCD中,底面ABCD是棱长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E,H分别是BC和PD上的中点.
如图,已知四棱锥P-ABCD中,底面ABCD是棱长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E,H分别是BC和PD上的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com