
A.命题“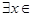 R使得 R使得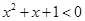 ”的否定是:“ ”的否定是:“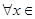 R均有 R均有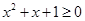 ”; ”; |
B.若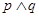 为假命题,则p,q均为假命题; 为假命题,则p,q均为假命题; |
C.若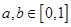 ,则不等式 ,则不等式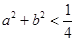 成立的概率是 成立的概率是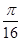 ; ; |
D.“平面向量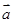 与 与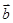 的夹角是钝角”的必要不充分条件是“ 的夹角是钝角”的必要不充分条件是“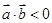 ”. ”. |
科目:高中数学 来源:不详 题型:单选题
| A.若a+b+c≠3,则a2+b2+c2<3 | B.若a+b+c=3,则a2+b2+c2<3 |
| C.若a+b+c≠3,则a2+b2+c2≥3 | D.若a2+b2+c2≥3,则a+b+c=3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.命题p、q均为假命题 |
| B.命题p、q均为真命题 |
| C.命题p、q中至少有一个是真命题 |
| D.命题p、q中至多有一个是真命题 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 为假命题,则
为假命题,则 与
与 均为假命题
均为假命题 有一组观测数据
有一组观测数据 ,其回归直线方程是
,其回归直线方程是 ,且
,且 ,则实数
,则实数
 与
与 它们的随机变量
它们的随机变量 的观测值
的观测值 来说
来说 越小.“
越小.“ 与
与 有关联”的把握程度越大
有关联”的把握程度越大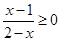 ,则函数
,则函数 的最小值为16. 其中真命题的个数为 ( )
的最小值为16. 其中真命题的个数为 ( )| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com