Question

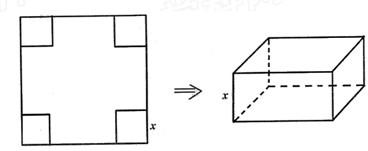
从边长为2a的正方形铁皮的四个角各截去一个边长为x的小正方形，再将四边向上折起，做成一个无盖的长方体铁盒，且要求长方体的高度x与底面正方形的边长的比不超过常数t．问：
（1）求长方体的容积V关于x的函数表达式；
（2）x取何值时，长方体的容积V有最大值？

Answer 1

分析：（1）先求出长方体的底面正方形的边长和高，便可求出长方体的容积V解析式．
（2）把容积V变形后使用基本不等式求出最大值，注意分析等号成立条件能否满足，
当等号成立条件不能满足时，利用导数值的符号确定函数的单调性，由单调性确定函数的最大值．

解答：解：（1）长方体的底面正方形的边长为2a-2x，高为x，所以，容积V=4（x-a）²x，
由

x

2a-2x

≤t，得 0＜x≤

2ta

1+2t

，
（2）由均值不等式知V=2（a-x）（a-x）（2x）≤2(

a-x+a-x+2x

3

)3=

16a3

27

，
当a-x=2x，即x=

a

3

时等号成立．
①当

a

3

≤

2ta

1+2t

，即t≥

1

4

，Vmax=

16a3

27

；
②当

a

3

＞

2ta

1+2t

，即0＜t＜

1

4

时，V′(x)=12(x-

2a

3

)2-

4a2

3

，
则V′（x）在(0，

a

3

)上单调递减，
∴V′(x)≥V′(

2ta

1+2t

)＞V′(

a

3

)=0，
∴V（x）在(0，

2ta

1+2t

]单调递增，
∴V(x)max=V(

2ta

1+2t

)=

8ta3

(1+2t)3

总之，若0＜t＜

1

4

，则当x=

2ta

1+2t

时，Vmax=

8ta3

(1+2t)3

；
若t≥

1

4

，则当x=

a

3

时，Vmax=

16a3

27

．

点评：本题考查基本不等式在函数最值中的应用，利用导数来研究函数的单调性，由函数的单调性确定函数的最大值．