练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知直线l过抛物线y2=2px(p＞0)的焦点F,且交于A、B两点，求|AB|的最小值.

    思路解析：设出适当的变量，建立关于|AB|的函数关系式，利用函数求最值.

    解法一：设直线l的方程是my=x-（m∈R），A（x1，y1），B（x2，y2），F（，0）.

    由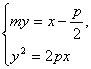得y2=2p（my+）.

    ∴y2-2pmy-p2=0.

    ∴y1+y2=2pm，y1y2=-p2.

    ∴|AB|=

    =

    =

    =

    =

    =2p（m∈R）

    =2p（1+m2）≥2p（1+0）=2p.

    ∴|AB|min=2p.

    解法二：设A（x1，y1），B（x2，y2）.

    则|AF|=x1+，|BF|=x2+.

    ∴|AB|=|AF|+|BF|=x1+x2+p.

    ∵y2=2px（p＞0）,

    ∴x1≥0,x2≥0.

    ∴x1+x2≥2.

    设直线l:my=x-(m∈R),

    由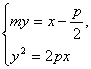得y2=2p(my+).

    ∴y2-2pmy-p2=0.∴y1+y2=2pm,y1y2=-p2.

    ∴x1x2=（my1+）（my2+）

    =m2y1y2+m(y1+y2)+

    =m2(-p2)+m(2pm)+

    =.

    ∴x1+x2≥2=p.

    ∴|AB|=x1+x2+p≥p+p=2p.

    ∴|AB|min=2p.

    解法三：如图所示.设直线l的倾斜角为θ，则直线l的方程是

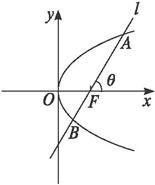
    ycosθ=（x-）sinθ.

    设A（x1，y1）、B（x2，y2），

    由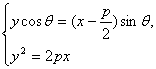消去y，得x2sin2θ-p（1+cos2θ）x+sin2θ=0,

    ∴x1+x2=.

    ∴|AB|=|AF|+|FB|=x1-+x2+=+p=≥2p.

    ∴|AB|min=2p.

    深化升华

        本题解答可以得到结论:通径是焦点弦长的最小值,即焦点弦长的最小值是通径长2p.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出下列命题：
    ①已知椭圆
    x2
    16
    +
    y2
    8
    =1    的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
    ②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
    ③若过双曲线C：
    x2
    a2
    -
    y2
    b2
    =1(a＞0，b＞0)    的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
    ④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
    其中正确命题的序号是
     
    ．（把你认为正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列命题：
    ①已知椭圆
    x2
    16
    +
    y2
    8
    =1两焦点F1，F2，则椭圆上存在六个不同点M，使得△F1MF2为直角三角形；
    ②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
    ③若过双曲线C：
    x2
    a2
    -
    y2
    b2
    =1（a＞0，b＞0）的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
    ④根据气象记录，知道荆门和襄阳两地一年中雨天所占的概率分别为20%和18%，两地同时下雨的概率为12%，则荆门为雨天时，襄阳也为雨天的概率是60%．
    其中正确命题的序号是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    给出下列命题：
    ①已知椭圆
    x2
    16
    +
    y2
    8
    =1    的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
    ②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
    ③若过双曲线C：
    x2
    a2
    -
    y2
    b2
    =1(a＞0，b＞0)    的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
    ④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
    其中正确命题的序号是______．（把你认为正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖北省襄阳四中、荆州中学、龙泉中学联考高二（下）期中数学试卷（理科）（解析版） 题型：选择题

    给出下列命题：
    ①已知椭圆=1两焦点F1，F2，则椭圆上存在六个不同点M，使得△F1MF2为直角三角形；
    ②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
    ③若过双曲线C：=1（a＞0，b＞0）的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
    ④根据气象记录，知道荆门和襄阳两地一年中雨天所占的概率分别为20%和18%，两地同时下雨的概率为12%，则荆门为雨天时，襄阳也为雨天的概率是60%．
    其中正确命题的序号是（ ）
    A．①③④
    B．①②③
    C．③④
    D．①②④

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年安徽省巢湖市高三（上）质量检测数学试卷（理科）（解析版） 题型：填空题

    给出下列命题：
    ①已知椭圆的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
    ②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
    ③若过双曲线C：的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
    ④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
    其中正确命题的序号是    ．（把你认为正确命题的序号都填上）

    查看答案和解析>>

    同步练习册答案