
(2007
北京朝阳模拟)如下图,棱长为1的正四面体ABCD中,E、F分别是棱AD、CD的中点,D是点A在平面BCD内的射影.(1)
求直线EF与直线BC所成角的大小;(2)
求点O到平面ACD的距离;(3)
求二面角A-BE-F的大小.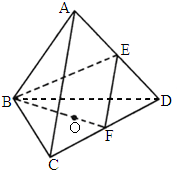
|
解析: (1)因为E、F分别是棱AD、CD的中点.所以EF∥AC.所以∠ BCA是EF与BC所成角.∵正四面体 ABCD,∴△ABC为正三角形,所以∠ BCA=60°.即 EF与BC所成角的大小是60°.(2) 如图,连结AO,AF,因为F是CD的中点,且△ACD,△BCD均为正三角形,所以 BF⊥CD,AF⊥CD.因为  ,所以CD⊥面AFB. ,所以CD⊥面AFB.
因为  面ACD.所以面AFB⊥面ACD. 面ACD.所以面AFB⊥面ACD.
因为 ABCD是正四面体,且O是点A在面BCD内的射影,所以点O必在正三角形BCD的中线BF上.在面 ABF中,过O做OG⊥AF,垂足为G.所以OG⊥面ACD.即 OG的长为点O到面ACD的距离.因为正四面体 ABCD的棱长为1,在△ ABF中,容易求出 , ,
因为△ AOF∽△OGF,故由相似比易求出 . .
所以点 O到平面ACD的距离是 . .
(3) 设△ABD中,AB边的中线交BE于H,连结CH,则由ABCD为正四面体知CH⊥面ABD.设 HD的中点为K,则FK∥CH.所以FK⊥面ABD.在面 ABD内,过点K作KN∥AD,KN交BE于M,交AB于N,因为 BE⊥AD,所以NM⊥BE.连结 FM,所以FM⊥BE.所以∠ NMF是所求二面角的平面角.
因为  , ,
所以  . .
所以  . .
所以所求二面角的大小为 
( 或者由正四面体的对称性,可转求二面角 的大小). 的大小). |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:022
(2007
北京朝阳模拟)将正奇数划分成下列组:(1),(3,5),(7,9,11),(13,15,17,19),…,则第n组各数的和是________,第n组的第一个数可以表示为_________.查看答案和解析>>
科目:高中数学 来源: 题型:044
(2007
北京朝阳模拟)已知 (a≠0)是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为(2,0),且f(x)在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(a≠0)是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为(2,0),且f(x)在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)
求c的值;(2)
在函数f(x)的图象上是否存在一点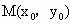 使得f(x)在点M处的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
使得f(x)在点M处的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
(3)
求|AC|的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:044
(2007
北京朝阳模拟)已知O为坐标原点,点E、F的坐标分别为(-1,0)、(1,0),动点A、M、N满足 (m>1),
(m>1),
 .
.
(1)
求点M的轨迹W的方程;(2)
点 在轨迹W上,直线PF交轨迹W于点Q,且
在轨迹W上,直线PF交轨迹W于点Q,且 ,若1≤λ≤2,求实数m的范围.
,若1≤λ≤2,求实数m的范围.查看答案和解析>>
科目:高中数学 来源: 题型:044
(2007
北京朝阳模拟)已知向量 ,
, ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足 ,其中O为坐标原点,k为参数.
,其中O为坐标原点,k为参数.
(1)
求动点M的轨迹方程,并判断曲线类型;(2)
如果动点M的轨迹是一条圆锥曲线,其离心率e满足 ,求实数k的取值范围.
,求实数k的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com