
【题目】如图所示,在三棱锥A﹣BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边且AD= ![]() ,BD=CD=1,另一侧面ABC是正三角形.
,BD=CD=1,另一侧面ABC是正三角形. 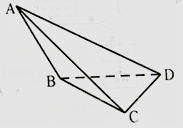
(1)求证:AD⊥BC;
(2)若在线段AC上存在一点E,使ED与平面BCD成30°角,试求二面角A﹣BD﹣E的大小.
【答案】
(1)证明:取BC的中点O,连结AO,DO,
∵BD=CD,AB=AC,
∴AO⊥BC,OD⊥BC,又OA∩OD=O,
∴BC⊥平面AOD,
又AD平面AOD,
∴AD⊥BC
(2)解:在平面AOD中,过O作OD的垂线Oz,则OC,OD,Oz两两垂直,
以O为原点,以OC,OD,Oz为坐标轴建立空间直角坐标系,如图所示:
∵BD=CD=1,AD= ![]() ,AC⊥CD,AB⊥BD,△ABC是等边三角形,
,AC⊥CD,AB⊥BD,△ABC是等边三角形,
∴BC=AB=AC= ![]() ,∴OD=
,∴OD= ![]() BC=
BC= ![]() ,OA=
,OA= ![]() ,
,
∴cos∠AOD= ![]() =﹣
=﹣ ![]() ,
,
∴A(0,﹣ ![]() ,1),C(
,1),C( ![]() ,0,0),D(0,
,0,0),D(0, ![]() ,0),
,0),
∴ ![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,1),
,1), ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,0),设
,0),设 ![]() =(﹣
=(﹣ ![]() λ,﹣
λ,﹣ ![]() λ,λ),
λ,λ),
则 ![]() =
= ![]() =(
=( ![]() ﹣
﹣ ![]() λ,﹣
λ,﹣ ![]() ﹣
﹣ ![]() λ,λ),
λ,λ),
∵平面BCD的一个法向量为 ![]() ,
,
∵ED与平面BCD成30°角,
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() ,解得λ=
,解得λ= ![]() ,
,
∴ ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,
, ![]() ),又B(﹣
),又B(﹣ ![]() ,0,0),
,0,0),
∴ ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,1),
,1), ![]() =(
=( ![]() ,
, ![]() ,0),
,0),
设平面BDE的法向量 ![]() =(x,y,z),则
=(x,y,z),则  ,即
,即 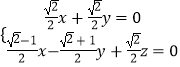 ,
,
令y=﹣1则 ![]() =(1,﹣1,﹣2),同理可得平面ABD的法向量为
=(1,﹣1,﹣2),同理可得平面ABD的法向量为 ![]() =(1,﹣1,﹣
=(1,﹣1,﹣ ![]() ),
),
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,设平面ABD与平面ACD成角为θ,
,设平面ABD与平面ACD成角为θ,
则 ![]() ,
,
∴ ![]() .
.

【解析】(1)取BC的中点O,连结AO,DO,由三线合一可得BC⊥OD,BC⊥AO,故而BC⊥平面AOD,于是BC⊥AD;(2)以O为原点建立空间坐标系,根据ED与平面BCD成30°角得出E点坐标,求出平面ABD与平面BDE的法向量,计算法向量的夹角即可得出二面角的大小.
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】若正态变量ξ服从正态分布N(μ,σ2),则ξ在区间(μ﹣σ,μ+σ),(μ﹣2σ,μ+2σ),(μ﹣3σ,μ+3σ)内取值的概率分别是0.6826,0.9544,0.9973.已知某大型企业为10000名员工定制工作服,设员工的身高(单位:cm)服从正态分布N(172,52),则适宜身高在177~182cm范围内员工穿的服装大约要定制套.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AB∥DC,∠BAD=90°,AB=AD= ![]() CD=1,如图2,将△ABD沿BD折起来,使平面ABD⊥平面BCD,设E为AD的中点,F为AC上一点,O为BD的中点.
CD=1,如图2,将△ABD沿BD折起来,使平面ABD⊥平面BCD,设E为AD的中点,F为AC上一点,O为BD的中点. 
(Ⅰ)求证:AO⊥平面BCD;、
(Ⅱ)若三棱锥A﹣BEF的体积为 ![]() ,求二面角A﹣BE﹣F的余弦值的绝对值.
,求二面角A﹣BE﹣F的余弦值的绝对值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个命题中,真命题是( ) ①从匀速传递的产品生产流水线上,质检员每30分钟从生产流水线中抽取一件产品进行某项指标检测,这样的抽样方法是系统抽样;
②两个变量的线性相关程度越强,则相关系数的值越接近于1;
③两个分类变量X与Y的观测值κ2 , 若κ2越小,则说明“X与Y有关系”的把握程度越大;
④随机变量X~N(0,1),则P(|X|<1)=2P(X<1)﹣1.
A.①④
B.②④
C.①③
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市卫生防疫部门为了控制某种病毒的传染,提供了批号分别为1,2,3,4,5的五批疫苗,供全市所辖的A,B,C三个区市民注射,每个区均能从中任选其中一个批号的疫苗接种.
(1)求三个区注射的疫苗批号中恰好有两个区相同的概率;
(2)记A,B,C三个区选择的疫苗批号的中位数为X,求 X的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}和{bn}的项数均为n,则将 ![]() 定义为数列{an}和{bn}的距离.
定义为数列{an}和{bn}的距离.
(1)已知 ![]() ,bn=2n+1,n∈N* , 求数列{an}和{bn}的距离dn .
,bn=2n+1,n∈N* , 求数列{an}和{bn}的距离dn .
(2)记A为满足递推关系 ![]() 的所有数列{an}的集合,数列{bn}和{cn}为A中的两个元素,且项数均为n.若b1=2,c1=3,数列{bn}和{cn}的距离大于2017,求n的最小值.
的所有数列{an}的集合,数列{bn}和{cn}为A中的两个元素,且项数均为n.若b1=2,c1=3,数列{bn}和{cn}的距离大于2017,求n的最小值.
(3)若存在常数M>0,对任意的n∈N* , 恒有 ![]() 则称数列{an}和{bn}的距离是有界的.若{an}与{an+1}的距离是有界的,求证:
则称数列{an}和{bn}的距离是有界的.若{an}与{an+1}的距离是有界的,求证: ![]() 与
与 ![]() 的距离是有界的.
的距离是有界的.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)若不等式f(x)﹣f(x+m)≤1恒成立,求实数m的最大值;
(2)当a< ![]() 时,函数g(x)=f(x)+|2x﹣1|有零点,求实数a的取值范围.
时,函数g(x)=f(x)+|2x﹣1|有零点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com