
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过
经过![]() ,
,![]() ,
,![]() 三点,
三点,![]() 是线段
是线段![]() 上的动点,
上的动点,![]() ,
,![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点.
两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 是使
是使![]() 恒成立的最小正整数.
恒成立的最小正整数.
①求![]() 的值;
的值;
②求三角形![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】
(1)确定出圆的圆心坐标,然后考虑直线![]() 的斜率是否存在,斜率存在时利用半弦长、半径、圆心到直线的距离构造成的直角三角形求解出直线的方程,注意验证是否符合;
的斜率是否存在,斜率存在时利用半弦长、半径、圆心到直线的距离构造成的直角三角形求解出直线的方程,注意验证是否符合;
(2) ①根据![]() 得到
得到![]() 的轨迹应该满足的条件,再将其转化为点到直线距离问题完成求解;
的轨迹应该满足的条件,再将其转化为点到直线距离问题完成求解;
②考虑分类讨论直线的斜率存在与否,并计算或表示出对应的面积,从而确定出面积的最小值.
(1)由题意可知,圆![]() 的直径为
的直径为![]() ,
,
所以圆![]() 方程为:
方程为:![]() .
.
因为![]() ,所以
,所以![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
若![]() 斜率不存在,则
斜率不存在,则![]() 到直线
到直线![]() 的距离为2,不符合,所以
的距离为2,不符合,所以![]() 斜率存在;
斜率存在;
设![]() 方程为:
方程为:![]() ,则
,则![]() ,解得
,解得![]() ,
,![]() ,
,
当![]() 时,直线
时,直线![]() 与
与![]() 轴无交点,不符合,舍去.
轴无交点,不符合,舍去.
所以![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
(2)①设![]() ,由点
,由点![]() 在线段
在线段![]() 上,得
上,得![]() ,即
,即![]() .
.
由![]() ,得
,得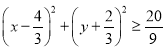 .
.
依题意知,线段![]() 与圆
与圆 至多有一个公共点,
至多有一个公共点,
故 ,解得
,解得![]() 或
或![]() .
.
因为![]() 是使
是使![]() 恒成立的最小正整数,所以
恒成立的最小正整数,所以![]() .
.
②![]() ,圆
,圆![]() 方程为:
方程为:![]() ,
,
(i)当直线![]() :
:![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,此时,
,此时,![]() ;
;
(ii)当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为:
的方程为:![]() ,
,
则![]() 的方程为:
的方程为:![]() ,点
,点![]() .所以,
.所以,![]() .
.
又圆心![]() 到
到![]() 的距离为
的距离为![]() ,
,
所以, .
.
故![]()
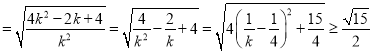 ,取等号时
,取等号时![]() .
.
又因为![]() ,所以三角形
,所以三角形![]() 面积的最小值为
面积的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某电力公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行综合排序,综合排序高者中标.
分值权重表如下:
总分 | 技术 | 商务 | 报价 |
100% | 50% | 10% | 40% |
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的.报价表则相对灵活,报价标的评分方法是:基准价的基准分是68分,若报价每高于基准价1%,则在基准分的基础上扣0.8分,最低得分48分;若报价每低于基准价1%,则在基准分的基础上加0.8分,最高得分为80分.若报价低于基准价15%以上(不含15%)每再低1%,在80分在基础上扣0.8分.
在某次招标中,若基准价为1000(万元).甲、乙两公司综合得分如下表:
公司 | 技术 | 商务 | 报价 |
甲 | 80分 | 90分 | A甲分 |
乙 | 70分 | 100分 | A乙分 |
甲公司报价为1100(万元),乙公司的报价为800(万元)则甲,乙公司的综合得分,分别是( )
A. 73,75.4B. 73,80C. 74.6,76D. 74.6,75.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() 左,右顶点分别为
左,右顶点分别为![]() ,
,![]() ,点
,点![]() ,
,![]() ,为椭圆
,为椭圆![]() 上位于
上位于![]() 轴上方的两点,且
轴上方的两点,且![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,记直线
,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于实数![]() 和两定点
和两定点![]() ,在某图形上恰有
,在某图形上恰有![]() 个不同的点
个不同的点![]() ,使得
,使得![]() ,称该图形满足“
,称该图形满足“![]() 度契合”.若边长为4的正方形
度契合”.若边长为4的正方形![]() 中,
中,![]() ,且该正方形满足“4度契合”,则实数
,且该正方形满足“4度契合”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 中点现将四边形
中点现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体在图②中,
,得到如图②所示的多面体在图②中,
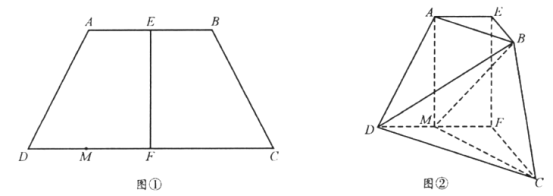
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,动点![]() 到两坐标轴的距离之和等于它到定点
到两坐标轴的距离之和等于它到定点![]() 的距离,记点P的轨迹为
的距离,记点P的轨迹为![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() 关于原点对称;②
关于原点对称;②![]() 关于直线
关于直线![]() 对称;③直线
对称;③直线![]() 与
与![]() 有无数个公共点;④在第一象限内,
有无数个公共点;④在第一象限内,![]() 与x轴和y轴所围成的封闭图形的面积小于
与x轴和y轴所围成的封闭图形的面积小于![]() .其中正确的结论是________.(写出所有正确结论的序号)
.其中正确的结论是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海湿地如图所示,A、B和C、D分别是以点O为中心在东西方向和南北方向设置的四个观测点,它们到点O的距离均为![]() 公里,实线PQST是一条观光长廊,其中,PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,QS段上的任意一点到中心点O的距离都相等,ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,以O为原点,AB所在直线为x轴建立平面直角坐标系xOy.
公里,实线PQST是一条观光长廊,其中,PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,QS段上的任意一点到中心点O的距离都相等,ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,以O为原点,AB所在直线为x轴建立平面直角坐标系xOy.
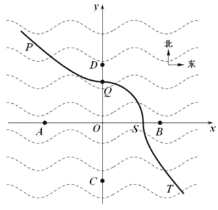
(1)求观光长廊PQST所在的曲线的方程;
(2)在观光长廊的PQ段上,需建一服务站M,使其到观测点A的距离最近,问如何设置服务站M的位置?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司推出一新款手机,因其功能强大,外观新潮,一上市便受到消费者争相抢购,销量呈上升趋势.散点图是该款手机上市后前6周的销售数据.
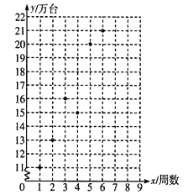
(Ⅰ)根据散点图,用最小二乘法求![]() 关于
关于![]() 的线性回归方程,并预测该款手机第8周的销量;
的线性回归方程,并预测该款手机第8周的销量;
(Ⅱ)为了分析市场趋势,该公司市场部从前6周的销售数据中随机抽取2周的数据,求抽到的这2周的销量均在20万台以下的概率.
参考公式:回归直线方程![]() ,其中:
,其中: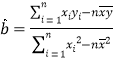 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数
有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数![]() 的取值范围是( )
的取值范围是( )
A. (![]() ,
,![]() ] B. (
] B. (![]() ,
,![]() ] C. [
] C. [![]() ,
,![]() ) D. [
) D. [![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com