
 ,左焦点
,左焦点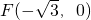 ,且离心率
,且离心率
 ,
,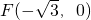 ,且离心率
,且离心率 ,
, ,
, ,
, .
. ,
, ,
, +(kx+m)2=1,
+(kx+m)2=1, +k2)x2+2kmx+m2-1=0,
+k2)x2+2kmx+m2-1=0, ,x1+x2=-
,x1+x2=- ,②
,② )+(1+k2)•
)+(1+k2)• +m2
+m2 k=0
k=0 k=0时 直线恒过点(
k=0时 直线恒过点( ,0)符合题意
,0)符合题意 ,0).
,0). ,
, ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程. ,由以MN为直径的圆经过椭圆C的右顶点A,知(2-x2)(2-x1)+y1y2=0,由y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,知4+(km-2)(x1+x2)+(1+k2)x1x2+m2=0.把y=kx+m代入椭圆方程
,由以MN为直径的圆经过椭圆C的右顶点A,知(2-x2)(2-x1)+y1y2=0,由y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,知4+(km-2)(x1+x2)+(1+k2)x1x2+m2=0.把y=kx+m代入椭圆方程 ,得(
,得( +k2)x2+2kmx+m2-1=0,再由韦达定理结合题设条件能求出该定点坐标.
+k2)x2+2kmx+m2-1=0,再由韦达定理结合题设条件能求出该定点坐标.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:2012-2013学年北京市高三第四次月考理科数学试卷(解析版) 题型:解答题
(本小题共14分)
已知椭圆C: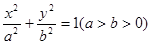 ,左焦点
,左焦点 ,且离心率
,且离心率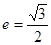
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线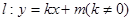 与椭圆C交于不同的两点
与椭圆C交于不同的两点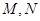 (
(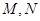 不是左、右顶点),且以
不是左、右顶点),且以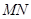 为直径的圆经过椭圆C的右顶点A. 求证:直线
为直径的圆经过椭圆C的右顶点A. 求证:直线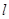 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源:北京月考题 题型:解答题
 的左焦点为F(﹣1,0),离心率为
的左焦点为F(﹣1,0),离心率为 ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省宜昌一中高二(上)期中数学试卷(文科)(解析版) 题型:解答题
 的左焦点为F(-1,0),离心率为
的左焦点为F(-1,0),离心率为 ,过点F的直线l与椭圆C交于A、B两点.
,过点F的直线l与椭圆C交于A、B两点.查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市海淀区北师特学校高三(上)第四次月考数学试卷(理科)(解析版) 题型:解答题
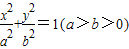 ,左焦点
,左焦点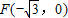 ,且离心率
,且离心率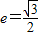
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com