

|


 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面
|

 所成的角为45°,底面ABCD为直角梯形,
所成的角为45°,底面ABCD为直角梯形,
|



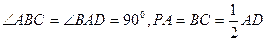
|
|
 (Ⅰ)求证:平面
(Ⅰ)求证:平面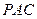 ⊥平面
⊥平面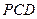 ;(Ⅱ)在棱
;(Ⅱ)在棱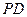 上是否存在一点
上是否存在一点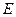 ,使
,使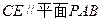 ?若存在,请确定E点的位置;若不存在,请说明理由.
?若存在,请确定E点的位置;若不存在,请说明理由.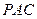 ⊥平面
⊥平面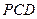

|
|


 (Ⅱ)分别以AB, AD, AP所在直线分别为x轴, y轴, z轴
(Ⅱ)分别以AB, AD, AP所在直线分别为x轴, y轴, z轴
|
 ∴ P(0, 0, 1), C(1, 1, 0), D(0, 2, 0).………… 8分
∴ P(0, 0, 1), C(1, 1, 0), D(0, 2, 0).………… 8分 |
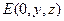 ,则
,则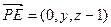 ,
,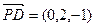 .…………………… 9分
.…………………… 9分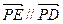 ,∴ y·(-1)-2 (z-1) =" 0" … ①…………………………… 10分
,∴ y·(-1)-2 (z-1) =" 0" … ①…………………………… 10分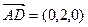 是平面
是平面 的法向量,…………………………… 11分
的法向量,…………………………… 11分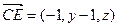 ,由
,由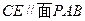 ,∴
,∴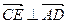 .…………………………… 12分
.…………………………… 12分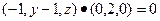 ,∴ y = 1,代入①得z = . …………………13分
,∴ y = 1,代入①得z = . …………………13分

科目:高中数学 来源:不详 题型:解答题
 是直角梯形,
是直角梯形,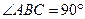 ,
,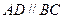 ,
,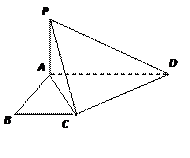
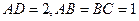 ,
, 平面
平面 .
.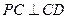 ;
;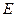 是
是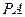 的中点,证明:
的中点,证明: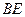 ∥平面
∥平面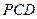 ;
;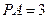 ,求三棱锥
,求三棱锥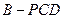 的体积.
的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.点P必在直线AC上 | B.点P必在直线BD上 |
| C.点P必在平面DBC外 | D.点P必在平面ABC内 |
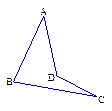
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
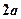 的正方体容器被水充满,首先把半径为
的正方体容器被水充满,首先把半径为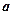 的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )
的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )A.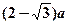 | B.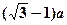 | C.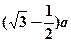 | D.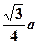 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com