分析:(1)利用b
n=S
n-S
n-1求出数列b
n的通项公式,然后利用
=4-(bn+2)求出数列a
n通项公式;
(2)利用c
n=a
nb
n.求出数列c
n的通项公式,写出前n项和T
n的表达式,利用错位相减法,求出前n项和T
n.
(3)求出数列c
n的最大值,利用
最大值≤m2+m-1,求出m的取值范围.
解答:解:(1)由已知和得,当n≥2时,
bn=Sn-Sn-1=(n2-n)-((n-1)2-(n-1))=3n-2(2分)
又b
1=1=3×1-2,符合上式.故数列b
n的通项公式b
n=3n-2.(3分)
又∵
=4-(bn+2),∴
an=4-=4-=()n,
故数列a
n的通项公式为
an=()n,(5分)
(2)
cn=anbn=(3n-2)•()n,
Sn=1×+4×()2+7×()3++(3n-2)×()n,①
Sn=1×()2+4×()3+7×()4++(3n-5)×()n+(3n-2)×()n+1,②
①-②得
Sn=+3×[()2+()3+()4++()n]-(3n-2)×()n+1=
+3×-(3n-2)×()n+1=
-(3n+2)×()n+1,
∴
Sn=-×()n+1. (10分)
(3)∵
cn=(3n-2)•()n,
∴
cn+1-cn=(3n+1)•()n+1-(3n-2)•()n=()n•[-(3n-2)]=
-9•()n+1(n-1),
当n=1时,c
n+1=c
n;当n≥2时,c
n+1≤c
n,∴
(cn)max=c1=c2=.
若
cn≤m2+m-1对一切正整数n恒成立,则
m2+m-1≥即可,
∴m
2+4m-5≥0,即m≤-5或m≥1. (14分).
点评:本题考查数列的通项公式的求法,数列求和等基础知识,考查计算能力、推理论证能力、综合发现问题解决问题的能力.



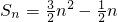 .数列an满足
.数列an满足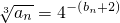 (n∈N*),数列cn满足cn=anbn.
(n∈N*),数列cn满足cn=anbn.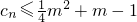 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围. .数列an满足
.数列an满足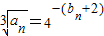 (n∈N*),数列cn满足cn=anbn.
(n∈N*),数列cn满足cn=anbn.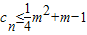 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.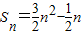 .数列an满足
.数列an满足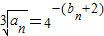 (n∈N*),数列cn满足cn=anbn.
(n∈N*),数列cn满足cn=anbn.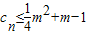 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.