
|
(Ⅱ)求二面角D—A1A—C的平面角的余弦值; (Ⅲ)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
(Ⅰ)见解析 (Ⅱ) ![]() (Ⅲ)存在
(Ⅲ)存在
连接BD交AC于O,则BD⊥AC,
连接A1O在△AA1O中,AA1=2,AO=1,
∠A1AO=60°∴A1O2=AA12+AO2-2AA1·Aocos60°=3
∴AO2+A1O2=A12∴A1O⊥AO,
由于平面AA1C1C⊥平面ABCD,所以A1O⊥底面ABCD
∴以OB、OC、OA1所在直线为x轴、y轴、z轴建立如图所示
空间直角坐标系,则A(0,-1,0),B(![]() ,0,0),C(0,1,0),
,0,0),C(0,1,0),
D(-![]() ,0,0),A1(0,0,
,0,0),A1(0,0,![]() )……2分
)……2分
(Ⅰ)由于![]()
![]() 则
则![]()
∴BD⊥AA1……4分
(Ⅱ)由于OB⊥平面AA1C1C∴平面AA1C1C的法向量![]()
设![]() ⊥平面AA1D则
⊥平面AA1D则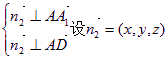 得到
得到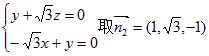 ……6分
……6分
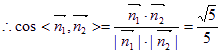 所以二面角D—A1A—C的平面角的余弦值是
所以二面角D—A1A—C的平面角的余弦值是![]() 8分
8分
(Ⅲ)假设在直线CC1上存在点P,使BP//平面DA1C1设![]() 则
则![]() 得
得![]() …9分
…9分
设![]() 则
则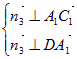 设
设![]()
得到 …………10分
…………10分
又因为![]() 平面DA1C1则
平面DA1C1则![]() ·
·![]()
即点P在C1C的延长线上且使C1C=CP……………………12分
法二:在A1作A1O⊥AC于点O,由于平面AA1C??1C⊥平面
ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD,
又底面为菱形,所以AC⊥BD
|
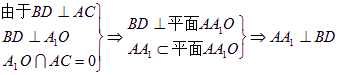
(Ⅱ)在△AA1O中,A1A=2,∠A1AO=60°
∴AO=AA1·cos60°=1
所以O是AC的中点,由于底面ABCD为菱形,所以
O也是BD中点
由(Ⅰ)可知DO⊥平面AA1C
过O作OE⊥AA1于E点,连接OE,则AA1⊥DE
则∠DEO为二面角D—AA1—C的平面角
……………………6分
在菱形ABCD中,AB=2,∠ABC=60°
∴AC=AB=BC=2∴AO=1,DO=![]()
在Rt△AEO中,OE=OA·sin∠EAO=![]()
DE=![]() ∴cos∠DEO=
∴cos∠DEO=![]()
∴二面角D—A1A—C的平面角的余弦值是![]() …………8分
…………8分
(Ⅲ)存在这样的点P连接B1C,因为A1B1![]() AB
AB![]() DC
DC
∴四边形A1B1CD为平行四边形。∴A1D//B1C
在C1C的延长线上取点P,使C1C=CP,连接BP……10分
因B??1??B![]() CC1,……12分∴BB1
CC1,……12分∴BB1![]() CP
CP
∴四边形BB1CP为平行四边形则BP//B1C∴BP//A1D∴BP//平面DA1C1


科目:高中数学 来源:2014届福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分13分) 如图,某观测站 在城
在城 的南偏西
的南偏西 的方向上,由
的方向上,由 城出发有一公路,走向是南偏东
城出发有一公路,走向是南偏东 ,在
,在 处测得距
处测得距 为31公里的公路上
为31公里的公路上 处,有一人正沿公路向
处,有一人正沿公路向 城走去,走了20公里后,到达
城走去,走了20公里后,到达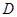 处,此时
处,此时 、
、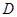 间距离为
间距离为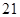 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达 城.
城.

查看答案和解析>>
科目:高中数学 来源:2014届福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分13分)如图,在平行六面体 中,
中,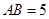 ,
, ,
, ,
, ,
, ,
, 是
是 的中点,设
的中点,设 ,
, ,
, .
.

(1)用 表示
表示 ;
;
(2)求 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修二空间点、直线、平面之间的位置关系练习卷(一) 题型:解答题
(本题满分13分)如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′—EC—B是直二面角.

(1)证明:BE⊥C D′;
(2)求二面角D′—BC—E的正切值.
查看答案和解析>>
科目:高中数学 来源:2013届湖北省武汉市高二下期末理科数学试卷(解析版) 题型:解答题
(本题满分13分)如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱 ,
, ,底面
,底面 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD,  ,O为AD中点.
,O为AD中点.

(1)求直线 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(2)求 点到平面
点到平面 的距离
的距离
(3)线段 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三5月月考调理科数学 题型:解答题
(本题满分13分)
如图,在三棱柱 中,已知
中,已知
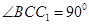 ,
,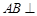 侧面
侧面
(1)求直线C1B与底面ABC所成角的正弦值;

(2)在棱 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若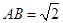 ,求二面角
,求二面角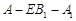 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com