
非空集合 关于运算
关于运算 满足:
满足:
(1)对任意 ,都有
,都有 ;
;
(2)存在 ,使得对一切
,使得对一切 ,都有
,都有 ,则称
,则称 关于运算
关于运算 为“融洽集”;现给出下列集合和运算:
为“融洽集”;现给出下列集合和运算:

 ① ②
① ②
③

 ④
④
 ⑤
⑤
其中 关于运算
关于运算 为“融洽集”____________。(写出所有“融洽集”的序号)
为“融洽集”____________。(写出所有“融洽集”的序号)
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
(2)存在![]() ,使得对一切
,使得对一切![]() ,都有
,都有![]() ,则称
,则称![]() 关于运算
关于运算![]() 为“融洽集”;现给出下列集合和运算:
为“融洽集”;现给出下列集合和运算:
①![]()
②![]()
③![]()
④![]()
⑤![]()
其中![]() 关于运算
关于运算![]() 为“融洽集”的是________________;(写出所有“融洽集”的序号)
为“融洽集”的是________________;(写出所有“融洽集”的序号)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市示范校高三12月综合练习(一)理科数学 题型:选择题
非空集合 关于运算
关于运算 满足:(1)对任意
满足:(1)对任意 、
、 ,都有
,都有 ;(2)存在
;(2)存在 ,使得对一切
,使得对一切 ,都有
,都有 ,则称
,则称 关于运算
关于运算 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:
① {非负整数},
{非负整数}, 为整数的加法。
为整数的加法。
② {偶数},
{偶数}, 为整数的乘法。
为整数的乘法。
③ {平面向量},
{平面向量}, 为平面向量的加法。
为平面向量的加法。
④ {二次三项式},
{二次三项式}, 为多项式的加法。
为多项式的加法。
其中 关于运算
关于运算 为“融洽集”的是( )
为“融洽集”的是( )
A.①② B.①③ C.②③ D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
非空集合![]() 关于运算
关于运算![]() 满足:(1)对任意
满足:(1)对任意![]() 、
、![]() ,都有
,都有![]() ;(2)存在
;(2)存在![]() ,使得对一切
,使得对一切![]() ,都有
,都有![]() ,则称
,则称![]() 关于运算
关于运算![]() 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:
①![]() {非负整数},
{非负整数},![]() 为整数的加法。
为整数的加法。
②![]() {偶数},
{偶数},![]() 为整数的乘法。
为整数的乘法。
③![]() {平面向量},
{平面向量},![]() 为平面向量的加法。
为平面向量的加法。
④![]() {二次三项式},
{二次三项式},![]() 为多项式的加法。
为多项式的加法。
其中![]() 关于运算
关于运算![]() 为“融洽集”的是( )
为“融洽集”的是( )
A.①② B.①③ C.②③ D.②④
查看答案和解析>>
科目:高中数学 来源:2012届北京市东城区普通高中示范校高三12月综合练习(一)理科数学 题型:单选题
非空集合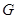 关于运算
关于运算 满足:(1)对任意
满足:(1)对任意 、
、 ,都有
,都有 ;(2)存在
;(2)存在 ,使得对一切
,使得对一切 ,都有
,都有 ,则称
,则称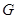 关于运算
关于运算 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:
① {非负整数},
{非负整数}, 为整数的加法。
为整数的加法。
② {偶数},
{偶数}, 为整数的乘法。
为整数的乘法。
③ {平面向量},
{平面向量}, 为平面向量的加法。
为平面向量的加法。
④ {二次三项式},
{二次三项式}, 为多项式的加法。
为多项式的加法。
其中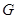 关于运算
关于运算 为“融洽集”的是( )
为“融洽集”的是( )
| A.①② | B.①③ | C.②③ | D.②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com