
给出下列三个结论:
(1)若命题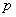 为假命题,命题
为假命题,命题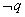 为假命题,则命题“
为假命题,则命题“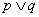 ”为假命题;
”为假命题;
(2)命题“若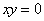 ,则
,则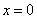 或
或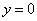 ”的否命题为“若
”的否命题为“若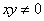 ,则
,则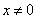 或
或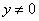 ”;
”;
(3)命题“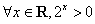 ”的否定是“
”的否定是“ 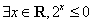 ”.则以上结论正确的个数为
”.则以上结论正确的个数为
A.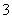 B.
B.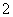 C.
C.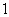 D.
D.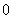
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
如图所示:一块椭圆形状的铁板 的长轴长为4米,短轴长为2米.
的长轴长为4米,短轴长为2米.
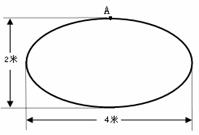 (1)若利用这块椭圆铁板
(1)若利用这块椭圆铁板 截取矩形,要求矩形的
截取矩形,要求矩形的
四个顶点都在椭圆铁板 的边缘,求所能截取
的边缘,求所能截取
的矩形面积的最大值;
(2)若以短轴的端点 为直角顶点,另外两个锐
为直角顶点,另外两个锐
角的顶点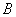 、
、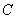 都在椭圆铁板的边缘,切割
都在椭圆铁板的边缘,切割
等腰直角三角形,则在不同的切割方案中,
共能切割出几个面积不同的等腰直角三角形?
最大面积是多少?(结果保留一位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com