直线l1:(m-2)x+3y+2m=0和l2:x+my+6=0,m为何值时
(1)l1∥l2;
(2)l1,l2重合;
(3)l1⊥l2.
【答案】
分析:(1)根据两直线平行时,直线方程中一次项系数之比相等,但不等于常数项之比,求得m的值.
(2)根据两直线重合时,直线方程中对应一次项系数之比相等,且都等于对应的常数项之比,从而求得m的值.
(3)根据两直线垂直时,一次项对应系数之积的和等于0,求得m的值.
解答:解:(1)∵直线l
1:(m-2)x+3y+2m=0和l
2:x+my+6=0,l
1∥l
2,由
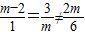
,求得m=-1.
(2)直线l
1:(m-2)x+3y+2m=0和l
2:x+my+6=0,l
1,l
2重合,则由
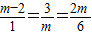
,求得 m=3.
(3)直线l
1:(m-2)x+3y+2m=0和l
2:x+my+6=0,l
1⊥l
2 ,则由(m-2)×1+3m=0,求得
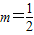 点评:
点评:本题主要考查两直线平行、重合、垂直的性质.两直线平行时,直线方程中一次项系数之比相等,但不等于常数项之比.两直线重合时,直线方程中对应一次项
系数之比相等,且都等于对应的常数项之比.两直线垂直时,一次项对应系数之积的和等于0,属于基础题.

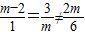 ,求得m=-1.
,求得m=-1.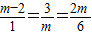 ,求得 m=3.
,求得 m=3.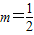


 通城学典默写能手系列答案
通城学典默写能手系列答案