解:(1)设x+1=t(t≠0),则x=t-1,
∴
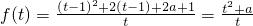
∴
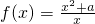
(2)当a=1时,
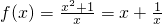
f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
证明:设0<x
1<x
2<1,则

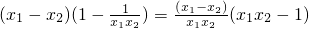
(8分)
∵0<x
1<x
2<1,∴x
1-x
2<0,x
1x
2>0,x
1x
2-1<0,
∴
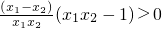
,∴f(x
1)-f(x
2)>0?f(x
1)>f(x
2)
所以,f(x)在(0,1)上单调递减,
同理可证得f(x)在(1,+∞)上单调递增
(3)∵
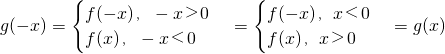
,
∴g(x)为偶函数,
所以,∴y=g(x)的图象关于y轴对称,
又当
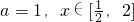
时,由(2)知

在

单调减,[1,2]单调增,
∴
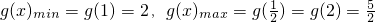
∴当a=1时,函数g(x)在区间
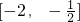
上的值域的为
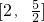
分析:(1)根据整体思想x+1=t(t≠0),则x=t-1,代入即可得到答案;(2)先把解析式化简后判断出单调性,再利用定义法证明:在区间上取值-作差-变形-判断符号-下结论,因解析式由分式,故变形时必须用通分.(3)根据题意判断出函数g(x)的奇偶性,根据(2)中函数的单调性,即可求出函数g(x)在区间
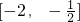
上的值域.
点评:本题考查了有关函数的性质综合题,用换元法求解析式,用定义法证明函数的奇偶性和单调性,必须遵循证明的步骤,考查了分析问题和解决问题能力.属中档题.

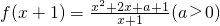 .
.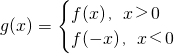 ,求函数g(x)在区间
,求函数g(x)在区间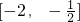 上的值域.
上的值域.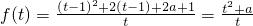
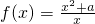
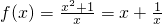

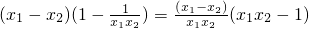 (8分)
(8分)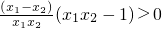 ,∴f(x1)-f(x2)>0?f(x1)>f(x2)
,∴f(x1)-f(x2)>0?f(x1)>f(x2)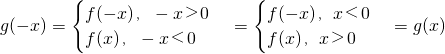 ,
,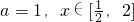 时,由(2)知
时,由(2)知 在
在 单调减,[1,2]单调增,
单调减,[1,2]单调增,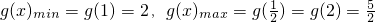
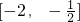 上的值域的为
上的值域的为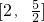
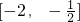 上的值域.
上的值域.
