
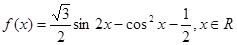
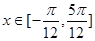 时,求函数
时,求函数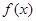 的最小值和最大值
的最小值和最大值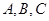 的对边分别为
的对边分别为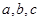 且
且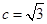 ,
,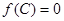 ,若
,若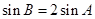 ,求
,求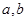 的值.
的值.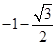 ,最大值为0;(2)
,最大值为0;(2)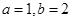 .
.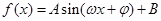 的形式后再解答;一般地,涉及三角函数的值域问题,多数情况下要将其变形为
的形式后再解答;一般地,涉及三角函数的值域问题,多数情况下要将其变形为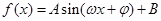 后,再利用三角函数的性质解答,也有部分题目,可转化为角的某个三角函数,然后用换元法转化为非三角函数问题;(2)由
后,再利用三角函数的性质解答,也有部分题目,可转化为角的某个三角函数,然后用换元法转化为非三角函数问题;(2)由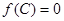 先求出
先求出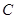 ,再利用正弦定理求出
,再利用正弦定理求出 ,再利用余弦定理则可求出
,再利用余弦定理则可求出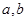 .在三角形中求角或边,通常对条件进行“统一”,统一为边或统一为角,主要的工具是正弦定理和余弦定理,同时不要忘记了三角形内角和定理.
.在三角形中求角或边,通常对条件进行“统一”,统一为边或统一为角,主要的工具是正弦定理和余弦定理,同时不要忘记了三角形内角和定理.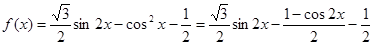
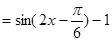 ,因为
,因为 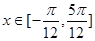 ,
,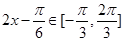 ,所以当
,所以当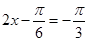 时,
时,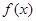 取得最小值
取得最小值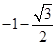 ,当
,当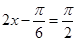 时,
时,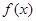 取得最大值0 6分
取得最大值0 6分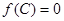 ,得
,得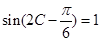 ,又
,又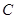 为三角形内角,所以
为三角形内角,所以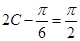 ,所以
,所以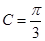 ,由正弦定理结合
,由正弦定理结合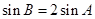 得,
得, ,再由余弦定理
,再由余弦定理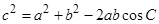 得,
得,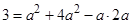 ,解得
,解得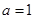 ,所以
,所以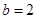 13分
13分

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com