
已知函数![]() ,
,![]()
![]() ,
,![]() 是参数,
是参数, ![]() ,
,![]() ,
,![]()
(1)、若![]() ,判别
,判别![]() 的奇偶性;
的奇偶性;
若![]() ,判别
,判别![]() 的奇偶性; (6分)
的奇偶性; (6分)
(2)、(理)若![]() ,
,![]() 是偶函数,求
是偶函数,求![]() (4分)
(4分)
(3)、请你仿照问题(1)(2)提一个问题(3),使得所提问题或是(1)的推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
将根据写出真命题所体现的思维层次和对问题探究的完整性,给予不同的评分。 (8分)
(1)解:![]() ,
,![]() 2分
2分
![]() ,
, ![]()
![]() 3分
3分
所以![]() 是偶函数 4分
是偶函数 4分

![]() 5分
5分
所以![]() 是非奇非偶函数 6分
是非奇非偶函数 6分
(2)(理)方法一(积化和差):![]() 为偶函数,
为偶函数,
![]() 8分
8分
![]() 为偶函数,所以
为偶函数,所以![]() 是偶函数, 9分
是偶函数, 9分
![]() ,
,![]() 10分
10分
方法二(定义法):![]() 为偶函数
为偶函数
所以![]()
展开整理![]() 对一切
对一切![]() 恒成立 8分
恒成立 8分
![]() ,
, ![]() 10分
10分
方法三(特殊值法):![]() 为偶函数
为偶函数
所以![]()
![]() 所以
所以![]() 8分
8分
![]() ,
, ![]() 10分
10分
(3)第一层次,写出任何一种的一个(加法或乘法)均可以, 13分
1、![]()
![]() 是偶函数; 2、
是偶函数; 2、![]()
![]() 是奇函数;
是奇函数;
3、![]()
![]() 是非奇非偶函数; 4、
是非奇非偶函数; 4、![]()
![]() 既奇又偶函数
既奇又偶函数
第二层次,写出任何一种的一个(加法或乘法)均可以, 14分
1、![]()
![]() 是偶函数 (数字不分奇偶)
是偶函数 (数字不分奇偶)
2、![]()
![]() 是奇函数
是奇函数![]()
![]() 是偶函数(数字只能同奇数)
是偶函数(数字只能同奇数)
3、![]()
![]() 是非奇非偶函数 (数字不分奇偶,但需相同)
是非奇非偶函数 (数字不分奇偶,但需相同)
4、![]()
![]() 是既奇又偶函数 (数字只能奇数)
是既奇又偶函数 (数字只能奇数)
![]()
![]() 是非奇非偶函数
是非奇非偶函数
第三层次,写出逆命题任何一种的一个(加法或乘法)均可以, 15分
1、![]() 是偶函数 (数字不分奇偶,但相同), 则
是偶函数 (数字不分奇偶,但相同), 则![]()
2、![]() 是奇函数 (数字只能正奇数) ,则
是奇函数 (数字只能正奇数) ,则 ![]()
![]() 是偶函数 (数字只能正偶数), 则
是偶函数 (数字只能正偶数), 则 ![]()
3、![]() 是偶函数 (数字只能正奇数),则
是偶函数 (数字只能正奇数),则![]()
第四层次,写出充要条件中的任何一种均可以, 16分
1、![]() 的充要条件是
的充要条件是![]() 是偶函数
是偶函数
2、![]() 是奇函数 (数字只能正奇数) 的充要条件是
是奇函数 (数字只能正奇数) 的充要条件是 ![]()
![]() 是偶函数 (数字只能正偶数)的充要条件是
是偶函数 (数字只能正偶数)的充要条件是 ![]()
3、![]() 是偶函数 (数字只能正奇数)的充要条件是 则
是偶函数 (数字只能正奇数)的充要条件是 则![]()
第五层次,写出任何一种均可以(逆命题,充要条件等均可以,限于篇幅省略) 18分
1、![]() 时,
时,![]() 都是偶函数
都是偶函数
2、![]() 时,
时,![]() 是正奇数,
是正奇数,![]() 是奇函数
是奇函数
![]() 时,
时,![]() 是正偶数,
是正偶数,![]() 是偶函数
是偶函数
3、![]() ,
,![]() 奇数,
奇数,![]() 既奇又偶函数
既奇又偶函数
4、![]() ,
,![]() 偶数,
偶数,![]() 是非奇非偶函数
是非奇非偶函数


科目:高中数学 来源:2011届上海市奉贤区高三4月调研测试理科数学 题型:解答题
、已知函数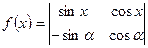 ,
,
 ,
,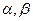 是参数,
是参数, 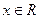 ,
,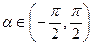 ,
,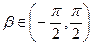
(1)、若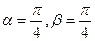 ,判别
,判别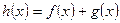 的奇偶性;
的奇偶性;
若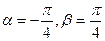 ,判别
,判别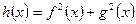 的奇偶性; (6分)
的奇偶性; (6分)
(2)、若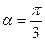 ,
,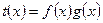 是偶函数,求
是偶函数,求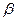 (4分)
(4分)
(3)、请你仿照问题(1)(2)提一个问题(3),使得所提问题或是(1)的 推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
将根据写出真命题所体现的思维层次和对问题探究的完整性,给予不同的评分。 (8分)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市奉贤区高三4月调研测试理科数学 题型:解答题
、已知函数 ,
,
 ,
, 是参数,
是参数,  ,
, ,
,
(1)、若 ,判别
,判别 的奇偶性;
的奇偶性;
若 ,判别
,判别 的奇偶性;
(6分)
的奇偶性;
(6分)
(2)、若 ,
, 是偶函数,求
是偶函数,求 (4分)
(4分)
(3)、请你仿照问题(1)(2)提一个问题(3),使得所提问题或是(1)的推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
将根据写出真命题所体现的思维层次和对问题探究的完整性,给予不同的评分。 (8分)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() ,
,![]()
![]() ,
,![]() 是参数,
是参数, ![]() ,
,![]() ,
,![]()
(1)、若![]() ,判别
,判别![]() 的奇偶性;
的奇偶性;
若![]() ,判别
,判别![]() 的奇偶性; (6分)
的奇偶性; (6分)
(2)、(理)若![]() ,
,![]() 是偶函数,求
是偶函数,求![]() (4分)
(4分)
(3)、请你仿照问题(1)(2)提一个问题(3),使得所提问题或是(1)的推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
将根据写出真命题所体现的思维层次和对问题探究的完整性,给予不同的评分。 (8分)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() ,
,![]()
![]() ,
,![]() 是参数,
是参数, ![]() ,
,![]() ,
,![]()
(1)、若![]() ,判别
,判别![]() 的奇偶性;
的奇偶性;
若![]() ,判别
,判别![]() 的奇偶性; (6分)
的奇偶性; (6分)
(2)、若![]() ,
,![]() 是偶函数,求
是偶函数,求![]() (4分)
(4分)
(3)、请你仿照问题(1)(2)提一个问题(3),使得所提问题或是(1)的推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
将根据写出真命题所体现的思维层次和对问题探究的完整性,给予不同的评分。 (8分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com