
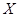 ,求
,求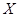 的分布列和数学期望.
的分布列和数学期望. 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源:不详 题型:解答题
 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)

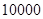 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨; 范围内的家庭中选出
范围内的家庭中选出 户作为采访对象,其中在
户作为采访对象,其中在 内的抽到
内的抽到 户,求
户,求 的分布列和期望
的分布列和期望 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
. 中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域
中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域 中的概率;
中的概率; 中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域
中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域 中的个数为
中的个数为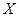 ,求
,求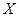 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,满足
,满足 电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.
电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 2列联表:
2列联表:| | 会围棋 | 不会围棋 | 总计 |
| 男 | | | |
| 女 | | | |
| 总计 | | | 30 |
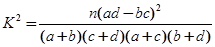 其中n=a+b+c+d
其中n=a+b+c+d | 0.40 | 0.25 | 0.10 | 0.010 |
 | 0.708 | 1.323 | 2.706 | 6.635 |
 ,求
,求 的期望.
的期望.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com