练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    有一种游戏规则如下：口袋里共装有4个红球和4个黄球，一次摸出4个，若颜色都相同，则
    得100分；若有3个球颜色相同，另一个不同，则得50分，其他情况不得分. 小张摸一次得分的期望是_____ .

    试题分析：小张摸一次得分的情况有100,50,0三种情况，当得分为100分时，概率为，当得分为50分时，概率为,所以期望为
    点评：解决排列组合问题时，要注意区分是排列还是组合，是有序还是无序，求离散型随机变量的期望，关键是求出它的分布列.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    在奥运会射箭决赛中，参赛号码为1～4号的四名射箭运动员参加射箭比赛.
    （Ⅰ）通过抽签将他们安排到1～4号靶位，试求恰有两名运动员所抽靶位号与其参赛号码相同的概率；
    （Ⅱ）记1号、2号射箭运动员射箭的环数为（所有取值为0，1，2，3．．．，10）的概率分别为、.根据教练员提供的资料，其概率分布如下表:

    		0
    		1
    		2
    		3
    		4
    		5
    		6
    		7
    		8
    		9
    		10

    		0
    		0
    		0
    		0
    		0.06
    		0.04
    		0.06
    		0.3
    		0.2
    		0.3
    		0.04

    		0
    		0
    		0
    		0
    		0.04
    		0.05
    		0.05
    		0.2
    		0.32
    		0.32
    		0.02
    ①1，2号运动员各射箭一次，求两人中至少有一人命中9环的概率；
    ②判断1号，2号射箭运动员谁射箭的水平高？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某校校庆，各届校友纷至沓来，某班共来了n位校友(n>8且n∈N*)，其中女校友6位，组委会对这n位校友登记制作了一份校友名单，现随机从中选出2位校友代表，若选出的2位校友是一男一女，则称为“最佳组合”．
    (1)若随机选出的2位校友代表为“最佳组合”的概率不小于，求n的最大值；
    (2)当n＝12时，设选出的2位校友代表中女校友人数为ξ，求ξ的分布列和数学期望E(ξ)．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    为了整顿道路交通秩序，某地考虑将对行人闯红灯进行处罚．为了了解市民的态度，在普通行人中随机选取了200人进行调查，得到如下数据：
    处罚金额x(元)
    		0
    		5
    		10
    		15
    		20
    会闯红灯的人数y
    		80
    		50
    		40
    		20
    		10
    若用表中数据所得频率代替概率．现从这5种处罚金额中随机抽取2种不同的金额进行处罚，在两个路口进行试验．
    (Ⅰ)求这两种金额之和不低于20元的概率；
    (Ⅱ)若用X表示这两种金额之和，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    抽签方式决定出场顺序.通过预赛，选拔出甲、乙等五支队伍参加决赛.
    (Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率；
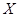    (Ⅱ)若决赛中甲队和乙队之间间隔的队伍数记为，求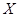的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某人上楼梯，每步上一阶的概率为，每步上二阶的概率为，设该人从台阶下的平台开始出发，到达第阶的概率为.
    (1)求；;
    (2)该人共走了5步，求该人这5步共上的阶数ξ的数学期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）某校举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛，答对3题者直接进入决赛，答错3题者则被淘汰，已知选手甲答题连续两次答错的概率为，（已知甲回答每个问题的正确率相同，并且相互之间没有影响。）（I）求甲选手回答一个问题的正确率；（Ⅱ）求选手甲可进入决赛的概率；（Ⅲ）设选手甲在初赛中答题的个数为，试写出的分布列，并求的数学期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    在一次数学考试中共有8道选择题，每道选择题都有4个选项，其中有且只有一个选项是正确的.某考生有5道题已选对正确答案，其余题中有两道只能分别判断2个选项是错误的，还有1道题因不理解题意只好乱猜.
    (1) 求该考生8道题全答对的概率；
    (2)若评分标准规定：“每题只选一个选项，选对得5分，不选或选错得0分”，求该考生所得分数的分布列.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知一袋有2个白球和4个黑球。
    （1）采用不放回地从袋中摸球（每次摸一球），4次摸球，求恰好摸到2个黑球的概率；
    （2）采用有放回从袋中摸球（每次摸一球），4次摸球，令X表示摸到黑球次数，
    求X的分布列和期望.

    查看答案和解析>>

    同步练习册答案