
有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙.已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.
据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
| 所用的时间(天数) | 10 | 11 | 12 | 13 |
| 通过公路1的频数 | 20 | 40 | 20 | 20 |
| 通过公路2的频数 | 10 | 40 | 40 | 10 |
 万元、
万元、 万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(Ⅰ)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.(注:毛利润=(销售商支付给生产商的费用)一(一次性费用)) .
万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(Ⅰ)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.(注:毛利润=(销售商支付给生产商的费用)一(一次性费用)) . (1)汽车B应选择公路2,汽车A应选择公路1
(2)汽车B为生产商获得毛利润更大
解析试题分析:(Ⅰ)频率分布表,如下:
科目:高中数学
来源:
题型:解答题
某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元。
科目:高中数学
来源:
题型:解答题
设函数
科目:高中数学
来源:
题型:解答题
一边长为
科目:高中数学
来源:
题型:解答题
经市场调查:生产某产品需投入年固定成本为3万元,每生产
科目:高中数学
来源:
题型:解答题
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为
科目:高中数学
来源:
题型:解答题
鑫隆房地产公司用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
2分所用的时间(天数) 10 11 12 13 通过公路1的频率 
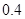


通过公路2的频率 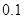
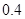
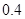
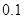
设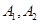 分别表示汽车A在前11天出发选择公路1、2将货物运往城市乙;
分别表示汽车A在前11天出发选择公路1、2将货物运往城市乙;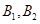 分别表示汽车B在前12天出发选择公路1、2将货物运往城市乙;
分别表示汽车B在前12天出发选择公路1、2将货物运往城市乙;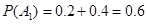 ,
,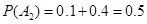 ,
,
所以汽车A应选择公路1,4分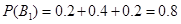 ,
,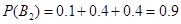 ,
,
所以汽车B应选择公路2.6分
(Ⅱ)设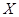 表示汽车A选择公路1时,销售商付给生产商的费用,则
表示汽车A选择公路1时,销售商付给生产商的费用,则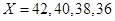 .
.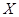 的分布列如下:
的分布列如下: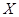
42 40 38 36 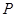




1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系: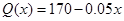 ,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本) ,
, 是定义域为R上的奇函数.
是定义域为R上的奇函数.
(1)求 的值,并证明当
的值,并证明当 时,函数
时,函数 是R上的增函数;
是R上的增函数;
(2)已知 ,函数
,函数 ,
, ,求
,求 的值域;
的值域;
(3)若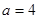 ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得 对
对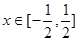 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数 ;若不存在,请说明理由.
;若不存在,请说明理由. 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。
(1)试把方盒的容积 表示为
表示为 的函数;
的函数;
(2) 多大时,方盒的容积
多大时,方盒的容积 最大?
最大?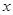 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,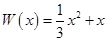 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,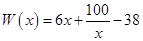 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(1)写出年利润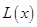 (万元)关于年产量
(万元)关于年产量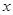 (万件)的函数解析式;
(万件)的函数解析式;
(注:年利润=年销售收入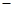 固定成本
固定成本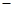 流动成本)
流动成本)
(2)年产量为多少万件时,在这一商品的生产中所获利润最大?最大利润是多少? 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
) 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号