
鑫隆房地产公司用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
科目:高中数学 来源: 题型:解答题
2013年,首都北京经历了59年来雾霾天气最多的一个月。经气象局统计,北京市从1月1日至1月30日这30天里有26天出现雾霾天气。《环境空气质量指数(AQI)技术规定(试行)》将空气质量指数分为六级:其中,中度污染(四级),指数为151—200;重度污染(五级),指数为201—300;严重污染(六级),指数大于300. 下面表1是该观测点记录的4天里,AQI指数 与当天的空气水平可见度
与当天的空气水平可见度 (千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果,
(千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果,
表1:AQI指数 与当天的空气水平可见度
与当天的空气水平可见度 (千米)情况
(千米)情况
AQI指数 |  |  |  |  |
空气可见度 (千米) (千米) |  |  |  |  |
| AQI指数 |  |  |  |  |  |
| 频数 | 3 | 6 | 12 | 6 | 3 |
 ,根据表1的数据,求出
,根据表1的数据,求出 关于
关于 的线性回归方程;
的线性回归方程;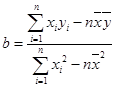 ,
, )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙.已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.
据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
| 所用的时间(天数) | 10 | 11 | 12 | 13 |
| 通过公路1的频数 | 20 | 40 | 20 | 20 |
| 通过公路2的频数 | 10 | 40 | 40 | 10 |
 万元、
万元、 万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(Ⅰ)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.(注:毛利润=(销售商支付给生产商的费用)一(一次性费用)) .
万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(Ⅰ)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.(注:毛利润=(销售商支付给生产商的费用)一(一次性费用)) .查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某医药研究所开发一种新药,在实验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量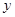 (微克)与时间
(微克)与时间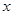 (小时)之间满足
(小时)之间满足 ,
,
其对应曲线(如图所示)过点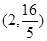 .
.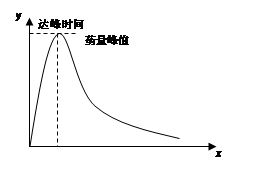
(1)试求药量峰值(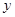 的最大值)与达峰时间(
的最大值)与达峰时间(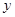 取最大值时对应的
取最大值时对应的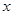 值);
值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间?(精确到0.01小时)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,在
,在 时取得极值.
时取得极值.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(Ⅲ)若 ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)设计一副宣传画,要求画面积为4840 ,画面的宽与高的比为
,画面的宽与高的比为 ,画面的上,下各留8
,画面的上,下各留8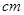 空白,左右各留5
空白,左右各留5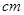 空白,怎样确定画面的高于宽尺寸,能使宣传画所用纸张面积最小?
空白,怎样确定画面的高于宽尺寸,能使宣传画所用纸张面积最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com