
已知 是定义在
是定义在  上的增函数,且对任意的
上的增函数,且对任意的 都满足
都满足 .
.
(Ⅰ)求 的值; (Ⅱ)若
的值; (Ⅱ)若 ,证明
,证明 ;
;
(Ⅲ)若 ,解不等式
,解不等式  .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
设函数 ,
, 是定义域为R上的奇函数.
是定义域为R上的奇函数.
(1)求 的值,并证明当
的值,并证明当 时,函数
时,函数 是R上的增函数;
是R上的增函数;
(2)已知 ,函数
,函数 ,
, ,求
,求 的值域;
的值域;
(3)若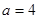 ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得 对
对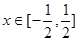 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
鑫隆房地产公司用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
已知关于x的方程x2+(m-3)x+m=0
(1)若此方程有实数根,求实数m的取值范围.
(2)若此方程的两实数根之差的绝对值小于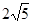 ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com