
已知二次函数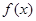 有两个零点
有两个零点 和
和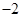 ,且
,且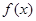 最小值是
最小值是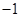 ,函数
,函数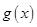 与
与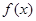 的图象关于原点对称;
的图象关于原点对称;
(1)求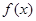 和
和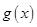 的解析式;
的解析式;
(2)若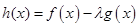 在区间
在区间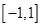 上是增函数,求实数
上是增函数,求实数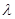 的取值范围。
的取值范围。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知二次函数 ,及函数
,及函数 。
。
关于 的不等式
的不等式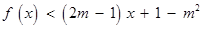 的解集为
的解集为 ,其中
,其中 为正常数。
为正常数。
(1)求 的值;
的值;
(2) R
R 如何取值时,函数
如何取值时,函数

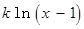 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若 ,且
,且
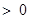 ,求证:
,求证:
 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
(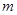 为常数,
为常数, ),且数列
),且数列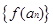 是首项为
是首项为 ,公差为
,公差为 的等差数列.
的等差数列.
(1) 若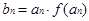 ,当
,当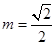 时,求数列
时,求数列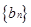 的前
的前 项和
项和 ;
;
(2)设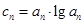 ,如果
,如果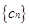 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求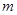 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某医药研究所开发一种新药,在实验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量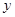 (微克)与时间
(微克)与时间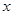 (小时)之间满足
(小时)之间满足 ,
,
其对应曲线(如图所示)过点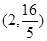 .
.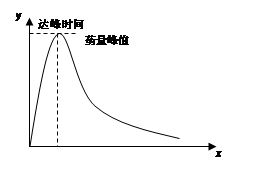
(1)试求药量峰值( 的最大值)与达峰时间(
的最大值)与达峰时间( 取最大值时对应的
取最大值时对应的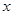 值);
值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间?(精确到0.01小时)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
(1)写出 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图1的一条折线表示;西红柿的种植成本与上市时间的关系用图2的抛物线表示.
(1)写出图1表示的市场售价与时间的函数关系式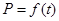 ;写出图2表示的种植成本与时间的函数关系式
;写出图2表示的种植成本与时间的函数关系式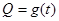 .
.
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
(注:市场售价和种植成本的单位:元/百千克,时间单位:天)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)某企业拟投资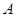 、
、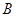 两个项目,预计投资
两个项目,预计投资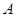 项目
项目 万元可获得利润
万元可获得利润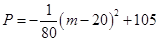
万元;投资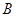 项目
项目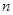 万元可获得利润
万元可获得利润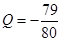
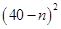
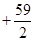
 万元.若该企业用40
万元.若该企业用40
万元来投资这两个项目,则分别投资多少万元能获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com