
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
(1)写出 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的 .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知x1、x2是关于x的一元二次方程x2+(3a-1)x+2a2-1=0的两个实数根,使得
(3x1-x2)(x1-3x2)=-80成立.求实数a的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店将进货价10元的商品按每个18元出售时,每天可卖出60个.商店经理到市场做了一番调研后发现,如将这种商品的售价(在每个18元的基础上)每提高1元,则日销售量就减少5个;如将这种商品的售价(在每个18元的基础上)每降低1元,则日销售量就增加10个.为获得每日最大的利润,此商品售价应定为每个多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现在人们经常使用电脑,若坐姿不正确,易造成眼睛疲劳,腰酸颈痛.一般正确的坐姿是:眼睛望向显示器屏幕时,应成20°的俯角α(即望向屏幕上边缘的水平视线与望向屏幕中心的视线的夹角);而小臂平放,肘部形成100°的钝角β.张燕家刚买的电脑显示器屏幕的高度为24.5cm,屏幕的上边缘到显示器支座底部的距离为36cm.已知张燕同学眼部到肩部的垂直距离为20cm,大臂长(肩部到肘部的距离)DE=28cm,张燕同学坐姿正确时肩部到臀部的距离是DM=53cm,请你帮张燕同学计算一下:
(1)她要按正确坐姿坐在电脑前,眼与显示器屏幕的距离应是多少?(精确到0.1cm)
(2)她要订做一套适合自己的电脑桌椅,桌、椅及键盘三者之间的高度应如何搭配?(精确到0.1cm) 
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某售报亭每天以每份0.4元的价格从报社购进若干份报纸,然后以每份1元的价格出售,如果当天卖不完,剩下的报纸以每份0.1元的价格卖给废品收购站.
(Ⅰ)若售报亭一天购进270份报纸,求当天的利润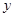 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:份,
(单位:份,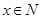 )的函数解析式.
)的函数解析式.
(Ⅱ)售报亭记录了100天报纸的日需求量(单位:份),整理得下表:
日需求量 | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
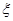 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求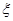 的数学期望;
的数学期望;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)一艘轮船在航行中每小时的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时8元,而其他与速度无关的费用是每小时128元.
(1)求轮船航行一小时的总费用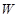 与它的航行速度
与它的航行速度 (公里/小时)的函数关系式;
(公里/小时)的函数关系式;
(2)问此轮船以多大的速度航行时,能使每公里的总费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com