
现在人们经常使用电脑,若坐姿不正确,易造成眼睛疲劳,腰酸颈痛.一般正确的坐姿是:眼睛望向显示器屏幕时,应成20°的俯角α(即望向屏幕上边缘的水平视线与望向屏幕中心的视线的夹角);而小臂平放,肘部形成100°的钝角β.张燕家刚买的电脑显示器屏幕的高度为24.5cm,屏幕的上边缘到显示器支座底部的距离为36cm.已知张燕同学眼部到肩部的垂直距离为20cm,大臂长(肩部到肘部的距离)DE=28cm,张燕同学坐姿正确时肩部到臀部的距离是DM=53cm,请你帮张燕同学计算一下:
(1)她要按正确坐姿坐在电脑前,眼与显示器屏幕的距离应是多少?(精确到0.1cm)
(2)她要订做一套适合自己的电脑桌椅,桌、椅及键盘三者之间的高度应如何搭配?(精确到0.1cm) 
(1)眼与显示器屏幕的距离约为33.7cm
(2)适合张燕同学的电脑桌应比椅子高出约37cm,键盘应比电脑桌低约11.6cm
解析试题分析:解:(1)由已知得BC="1" 2 ×24.5=12.25(cm) 1分
在Rt△ABC中,tanα="BC/" AC ,
∴AC="BC" tan20° ≈33.7(cm) 3分
即眼与显示器屏幕的距离约为33.7cm; 4分
(2)如图,过点D、E分别作AC的平行线和垂线,相交于点F,
则∠DEF=100°-90°=10°, 6分
在Rt△DEF中,cos10°="FE" /DE ,
∴FE=DE•cos10°=28•cos10°≈27.57(cm), 7分
∴电脑桌与键盘的高度之差约为
20+27.57-36=11.6(cm).
电脑桌与电脑椅的高度之差为约为
20+53-36=37(cm).
因此,适合张燕同学的电脑桌应比椅子高出约37cm,键盘应比电脑桌低约11.6cm. 9分
考点:三角函数值的运用
点评:解决的关键是能结合三角函数值来表示高度差,属于基础题。


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:解答题
如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为多少时,盒子容积最大,并求出此最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
提高大桥的车辆通行能力可改善整个城市的交通状况.一般情况下,大桥上的车流
速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当车流密度不超过50辆/千米时,车流速度为30千米/小时.研究表明:当50<x≤200时,车流速度v与车流密度x满足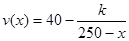 .当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
(Ⅰ)当0<x≤200时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上观测点的车辆数,单位:
辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到个位,参考数据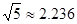 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
(1)写出 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地政府鉴于某种日常食品价格增长过快,欲将这种食品价格控制在适当范围内,决定对这种食品生产厂家提供政府补贴,设这种食品的市场价格为 元/千克,政府补贴为
元/千克,政府补贴为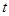 元/千克,根据市场调查,当
元/千克,根据市场调查,当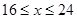 时,这种食品市场日供应量
时,这种食品市场日供应量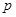 万千克与市场日需量
万千克与市场日需量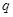 万千克近似地满足关系:
万千克近似地满足关系: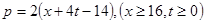 ,
,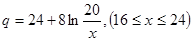 。当
。当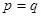 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。
(1)将政府补贴表示为市场平衡价格的函数,并求出函数的值域;
(2)为使市场平衡价格不高于每千克20元,政府补贴至少为每千克多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图1的一条折线表示;西红柿的种植成本与上市时间的关系用图2的抛物线表示.
(1)写出图1表示的市场售价与时间的函数关系式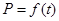 ;写出图2表示的种植成本与时间的函数关系式
;写出图2表示的种植成本与时间的函数关系式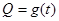 .
.
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
(注:市场售价和种植成本的单位:元/百千克,时间单位:天)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分15分)
经过长期的观测得到:在交通繁忙时段,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为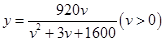 .
.
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.已知凹槽的强度与横截面的面积成正比,比例系数为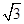 ,设AB=2x,BC=y.
,设AB=2x,BC=y.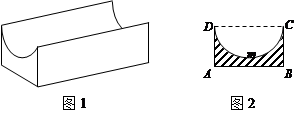
(1)写出y关于x函数表达式,并指出x的取值范围;
(2)求当x取何值时,凹槽的强度最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com