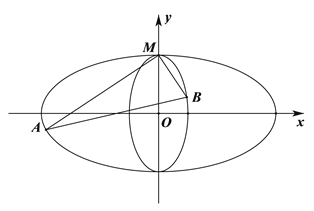
[题目]如图.焦点在轴上的椭圆与焦点在轴上的椭圆都过点.中心都在坐标原点.且椭圆与的离心率均为．(Ⅰ)求椭圆与椭圆的标准方程,(Ⅱ)过点M的互相垂直的两直线分别与.交于点A.B(点A.B不同于点M).当的面积取最大值时.求两直线MA.MB斜率的比值. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，焦点在轴上的椭圆与焦点在轴上的椭圆都过点，中心都在坐标原点，且椭圆与的离心率均为．

（Ⅰ）求椭圆与椭圆的标准方程；

（Ⅱ）过点M的互相垂直的两直线分别与，交于点A，B（点A、B不同于点M），当的面积取最大值时，求两直线MA，MB斜率的比值.

【答案】（1），（2）

【解析】分析：(1)根据题的条件，得到对应的椭圆的上顶点，即可以求得椭圆中相应的参数，结合椭圆的离心率的大小，求得相应的参数，从而求得椭圆的方程；

(2)设出一条直线的方程，与椭圆的方程联立，消元，利用求根公式求得对应点的坐标，进一步求得向量的坐标，将S表示为关于k的函数关系，从眼角函数的角度去求最值，从而求得结果.

详解：（Ⅰ）依题意得对：，，得：；

同理：.

（Ⅱ）设直线的斜率分别为，则MA：，与椭圆方程联立得：

，得，得,，所以

同理可得.所以,

从而可以求得因为，

所以，不妨设

，所以当最大时，，此时两直线MA，MB斜率的比值.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

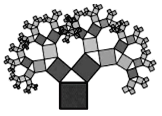
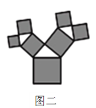
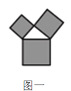
【题目】如图是美丽的“勾股树”，它是一个直角三角形分别以它的每一边向外作正方形而得到.图一是第1代“勾股树”，重复图一的作法，得到图二为第2代“勾股树”，以此类推，已知最大的正方形面积为1，则第n代“勾股树”所有正方形的面积的和为（）

A. nB. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥中，⊥底面，⊥，∥，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点．

（1）证明：BE⊥DC；

（2）若F为棱PC上一点，满足BF⊥AC，求二面角F－AB－P的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数其中P，M是非空数集．记f(P）＝{y|y＝f(x)，x∈P}，f(M)＝{y|y＝f(x)，x∈M}．

（Ⅰ）若P＝[0，3]，M＝(﹣∞，﹣1)，求f(P)∪f(M)；

（Ⅱ）若P∩M＝，且f(x)是定义在R上的增函数，求集合P，M；

（Ⅲ）判断命题“若P∪M≠R，则f(P)∪f(M)≠R”的真假，并加以证明．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】等腰直角三角形的斜边AB为正四面体侧棱，直角边AE绕斜边AB旋转，则在旋转的过程中，有下列说法：

（1）四面体EBCD的体积有最大值和最小值；

（2）存在某个位置，使得；

（3）设二面角的平面角为，则；

（4）AE的中点M与AB的中点N连线交平面BCD于点P，则点P的轨迹为椭圆.

其中，正确说法的个数是（）

A. 1 B. 2 C. 3 D. 4

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列是首项为1的等差数列，数列满足，且.

（1）求数列的通项公式；

（2）令，求数列的前项和.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】脐橙营养丰富，含有人体所必需的各类营养成份，若规定单个脐橙重量（单位：千克）在[0.1，0.3）的脐橙是“普通果”，重量在[0.3，0.5）的磨橙是“精品果”，重量在[0.5，0.7]的脐橙是“特级果”，有一果农今年种植脐橙，大获丰收为了了解脐橙的品质，随机摘取100个脐橙进行检测，其重量分别在[0.1，0.2），[0.2，0.3），[0.3，0.4），[0.4，0.5），[0.5，0.6），[0.6，0.7]中，经统计得到如图所示频率分布直方图

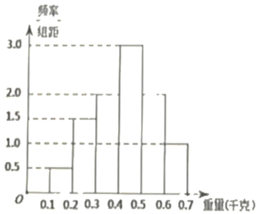
（1）将频率视为概率，用样本估计总体．现有一名消费者从脐橙果园中，随机摘取5个脐橙，求恰有3个是“精品果”的概率．

（2）现从摘取的100个脐橙中，采用分层抽样的方式从重量为[0.4，0.5），[0.5，0.6）的脐橙中随机抽取10个，再从这10个抽取3个，记随机变量X表示重量在[0.5，0.6）内的脐橙个数，求X的分布列及数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】条形码是将宽度不等的多个黑条和空白，按照一定的编码规则排列，用以表达一组信息的图形标识符。常见的条形码是“”通用代码，它是由从左到右排列的13个数字（用表示）组成，其中是校验码，用来校验前12个数字代码的正确性.下面的框图是计算第13位校验码的程序框图，框图中符号表示不超过的最大整数(例如).现有一条形码如图（1)所示,其中第6个数被污损，那么这个被污损数字是（）