练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．有三张卡片，分别写有1和2，1和3，2和3，甲乙丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上没有的数字是（　　）
    A．不确定B．3C．2D．1

    分析 可先根据丙的说法推出丙的卡片上写着1和2，或1和3，分别讨论这两种情况，根据甲和乙的说法可分别推出甲和乙卡片上的数字，这样便可判断出甲卡片上的数字是多少．

    解答 解：根据丙的说法知，丙的卡片上写着1和2，或1和3；
    （1）若丙的卡片上写着1和2，根据乙的说法知，乙的卡片上写着2和3；
    ∴根据甲的说法知，甲的卡片上写着1和3；
    （2）若丙的卡片上写着1和3，根据乙的说法知，乙的卡片上写着2和3；
    又甲说，“我与乙的卡片上相同的数字不是2”；
    ∴甲的卡片上写的数字不是1和2，这与已知矛盾；
    ∴甲的卡片上的数字是1和3．
    故选C．

    点评 考查进行简单的合情推理的能力，以及分类讨论的解题思想，做这类题注意找出解题的突破口．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．若圆（x-3）2+y2=1上只有一点到双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线的距离为1，则该双曲线离心率为（　　）
    A．$\frac{{3\sqrt{5}}}{5}$B．$\frac{{3\sqrt{3}}}{4}$C．$\sqrt{3}$D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

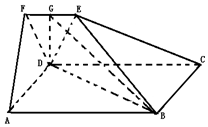    5．如图，在五面体ABCDEF中，四边形ABCD为正方形，EF∥CD，平面CDFE⊥平面ABCD，且AD=3EF，DE=DF，点G为EF中点．
    （Ⅰ）求证：DG⊥BC；
    （Ⅱ）M是线段BD上一点，若GM∥平面ADF，求DM：MB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知圆锥的底面半径和高均为1，则该圆锥的侧面积为$\sqrt{2}π$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设z∈C且z≠0，“z是纯虚数”是“z2∈R”的（　　）
    A．充分非必要条件B．必要非充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．16、（文）函数$f（x）=1+\frac{sinx}{{{x^2}+1}}$的最大值为 M，最小值为m，则 M+m=  2  ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．在平面直角坐标系xOy中，动点P（x，y）到两坐标轴的距离之和等于它到定点（1，1）的距离，记点P的轨迹为C．给出下面四个结论：
    ①曲线C关于原点对称；
    ②曲线C关于直线y=x对称；
    ③点（-a2，1）（a∈R）在曲线C上；
    ④在第一象限内，曲线C与x轴的非负半轴、y轴的非负半轴围成的封闭图形的面积小于$\frac{1}{2}$．
    其中所有正确结论的序号是②③④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设数列{an}的前n项和为Sn，若Sn+1=2an+1，n∈N*，则a3=（　　）
    A．3B．2C．1D．0

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年江西省南昌市高二文下学期期末考试数学试卷（解析版） 题型：选择题

    设函数的图像与的图像关于直线对称，且，则（ ）

    A． B． C． D．

    查看答案和解析>>

    同步练习册答案