
甲、乙两人在罚球线互不影响地投球,命中的概率分别为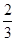 与
与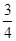 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.
(1)甲、乙两人在罚球线各投球一次,求两人得分之和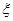 的数学期望;
的数学期望;
(2)甲、乙两人在罚球线各投球二次,求甲恰好比乙多得分的概率.
(1)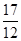
(2)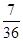
【解析】
试题分析:解:(1)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,则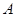 与
与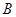 相互独立,且P(A)=
相互独立,且P(A)= ,P(B)=
,P(B)= ,P(
,P(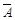 )=
)=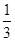 ,P(
,P(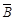 )=
)=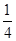 . 1分
. 1分
甲、乙两人得分之和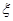 的可能取值为0、1、2, 2分
的可能取值为0、1、2, 2分
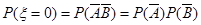
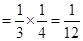
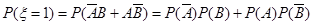
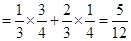
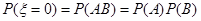
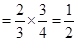 4分
4分
则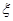 概率分布为:
概率分布为:
|
|
0 |
1 |
2 |
|
|
|
|
|
5分
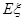 =0×
=0×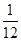 +1×
+1×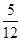 +2×
+2×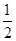 =
=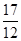 . 6分
. 6分
答:每人在罚球线各投球一次,两人得分之和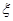 的数学期望为
的数学期望为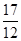 .
7分
.
7分
(2)设甲恰好比乙多得分为事件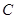 ,甲得分且乙得
,甲得分且乙得 分为事件
分为事件 ,甲得
,甲得 分且乙得分为事件
分且乙得分为事件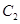 ,则
,则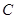 =
= +
+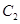 ,且
,且 与
与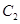 为互斥事件. 8分
为互斥事件. 8分
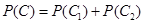
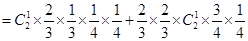
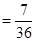 11分
11分
答:甲、乙两人在罚球线各投球二次,甲恰好比乙多得分的概率为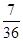 。 12分
。 12分
考点:分布列和独立事件的概率
点评:主要是通过实际问题来考查同学们运用概率公式来求解事件发生的概率以及分布列的运用,属于中档题。


科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 与
与 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.查看答案和解析>>
科目:高中数学 来源:韶关二模 题型:解答题
| 2 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:韶关二模 题型:解答题
| 2 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com