
(本题12分)已知数列 满足
满足 .是否存在等差数列
.是否存在等差数列 ,使得数列
,使得数列 与
与 满足
满足 对一切正整数
对一切正整数 成立? 证明你的结论.
成立? 证明你的结论.
A
【解析】令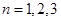 ,有
,有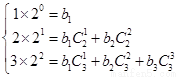 ,即
,即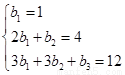 ,
,
解得 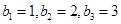 .
由此猜想:
.
由此猜想: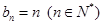 . ----------------4分
. ----------------4分
下面证明: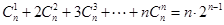 .
.
解法一:设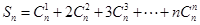
有 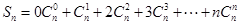
又 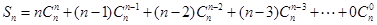 ------------8分
------------8分
两式相加 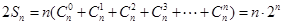 ------------10分
------------10分
故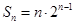 ,即
,即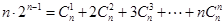 .
------------12分
.
------------12分
解法二:构造函数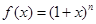 ,
,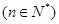 ,由二项式定理,知
,由二项式定理,知
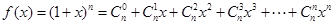 ,
-------------------8分
,
-------------------8分
对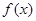 求导,得
求导,得 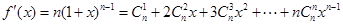 ---10分
---10分
令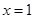 ,即得
,即得 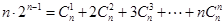 .
-------------------12分
.
-------------------12分
解法三:⑴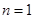 时,
时,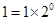 成立.
--------------------------5分
成立.
--------------------------5分
⑵假设当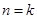 时等式成立,即
时等式成立,即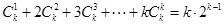 .
.
当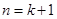 时,
时, 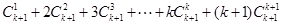
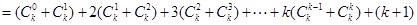
--------------------------------8分
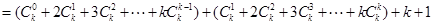
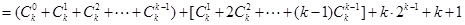
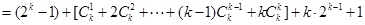
--------------------10分
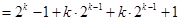
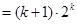
也就是说,当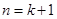 时,等式也成立.
时,等式也成立.
由⑴⑵可知,存在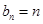 ,使得
,使得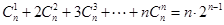 对一切
对一切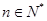 成立.
---------------------12分
成立.
---------------------12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(本题12分)已知数列![]() 是等差数列,a2 = 3,a5 = 6,数列
是等差数列,a2 = 3,a5 = 6,数列![]() 的前n项和是Tn,且Tn +
的前n项和是Tn,且Tn +![]() .
.
![]() (1)求数列
(1)求数列![]() 的通项公式与前n项的和Mn;
的通项公式与前n项的和Mn;
![]() (2)求数列
(2)求数列![]() 的通项公式;
的通项公式;
(3)记cn =![]() ,求
,求![]() 的前n项和Sn.
的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2011届山东省济宁市一中高三年级第二次质量检测数学文卷 题型:解答题
(本题12分)
已知数列 的前n项和为
的前n项和为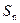 ,且满足
,且满足 ,
,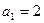
(1)求证: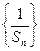 是等差数列;
是等差数列;
(2)求 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源:2012届甘肃省兰州一中高三上学期期中考试理科数学试卷 题型:解答题
(本题12分)已知数列{an}中,a1=0,a2 =4,且an+2-3an+1+2an= 2n+1( ),
),
数列{bn}满足bn=an+1-2an.
(Ⅰ)求证:数列{ -
-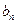 }是等比数列;
}是等比数列;
(Ⅱ)求数列{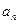 }的通项公式;
}的通项公式;
(Ⅲ)求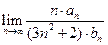 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省襄樊四校高三期中考试理科数学试卷 题型:解答题
(本题12分)已知数列 的前
的前 项和
项和 ,且
,且 是
是 和1的等差中项。
和1的等差中项。
(1)求数列 与
与 的通项公式;
的通项公式;
(2)若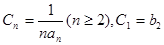 ,求
,求 ;
;
(3)若 是否存在
是否存在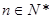 ,使
,使 ?说明理由。
?说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省襄樊四校高三期中考试文科数学试卷 题型:解答题
(本题12分)已知数列 的前
的前 项和
项和 且
且 是
是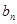 和1的等差中项。
和1的等差中项。
(1)求数列 与
与 的通项公式;
的通项公式;
(2)若 ,求
,求 ;
;
(3)若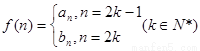 是否存在
是否存在 ,使
,使 ?说明理由。
?说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com