
分析 (1)由题意${δ_1}=\frac{x-2y}{{\sqrt{5}}}$、${δ_2}=\frac{x+2y}{{\sqrt{5}}}$,于是${δ_1}{δ_2}=\frac{{{x^2}-4{y^2}}}{5}=\frac{{2{x^2}-4}}{5}$,又-2≤x≤2得0≤x2≤4,即可求δ1δ2的取值范围.
(2)由题意${η_1}=\frac{-tcosα-2}{{\sqrt{{{cos}^2}α+4{{sin}^2}α}}}$,${η_2}=\frac{tcosα-2}{{\sqrt{{{cos}^2}α+4{{sin}^2}α}}}$,于是${η_1}{η_2}=\frac{(tcosα-2)(-tcosα-2)}{{{{cos}^2}α+4{{sin}^2}α}}=1$,可得4-t2cos2α=cos2α+4sin2α?(3-t2)cos2α=0对任意的α都成立,即可得出结论;
(3)确定n2>b2+m2a2,$A(-\frac{n}{m},0)$,B(0,n)$|AB{|^2}=\frac{n^2}{m^2}+{n^2}$,即可比较|AB|的长与a+b的大小.
解答 解:(1)由点P(x,y)在椭圆$\frac{x^2}{4}+{y^2}=1$上,所以${y^2}=1-\frac{x^2}{4}$
由题意${δ_1}=\frac{x-2y}{{\sqrt{5}}}$、${δ_2}=\frac{x+2y}{{\sqrt{5}}}$,于是${δ_1}{δ_2}=\frac{{{x^2}-4{y^2}}}{5}=\frac{{2{x^2}-4}}{5}$ 2分
又-2≤x≤2得0≤x2≤4,即$-\frac{4}{5}≤{δ_1}{δ_2}≤\frac{4}{5}$ 4分
(2)假设存在实数t,满足题设,
由题意${η_1}=\frac{-tcosα-2}{{\sqrt{{{cos}^2}α+4{{sin}^2}α}}}$,${η_2}=\frac{tcosα-2}{{\sqrt{{{cos}^2}α+4{{sin}^2}α}}}$,
于是${η_1}{η_2}=\frac{(tcosα-2)(-tcosα-2)}{{{{cos}^2}α+4{{sin}^2}α}}=1$ 6分
4-t2cos2α=cos2α+4sin2α?(3-t2)cos2α=0对任意的α都成立
只要3-t2=0即可,所以$t=±\sqrt{3}$
故存在实数t,$t=±\sqrt{3}$,对任意的α都有η1η2=1成立. 9分
(3)设F1,F2的坐标分别为(-c,0)、(c,0),于是c2=a2-b2
${λ_1}=\frac{-mc+n}{{\sqrt{1+{m^2}}}}$、${λ_2}=\frac{mc+n}{{\sqrt{1+{m^2}}}}$于是${λ_1}{λ_2}=\frac{{{n^2}-{m^2}{c^2}}}{{1+{m^2}}}>{b^2}$⇒n2>b2+m2a2
又$A(-\frac{n}{m},0)$,B(0,n)即$|AB{|^2}=\frac{n^2}{m^2}+{n^2}$ 12分
所以$\frac{n^2}{m^2}+{n^2}>{a^2}+\frac{b^2}{m^2}+{b^2}+{m^2}{a^2}≥{a^2}+{b^2}+2ab={(a+b)^2}$
综上|AB|>a+b. 14分
点评 本题考查推理,考查新定义,考查学生分析解决问题的能力,难度大.


科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{π}{6}})$ | B. | $({\frac{π}{6},\frac{π}{4}})$ | C. | $({\frac{π}{4},\frac{π}{3}})$ | D. | $({\frac{π}{3},\frac{π}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
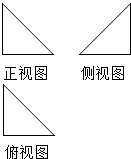 一个空间几何体的三视图如图所示,其正视图、侧视 图、俯视图均为等腰直角三角形,且直角边长都为1,则它的外接球的表面积是( )
一个空间几何体的三视图如图所示,其正视图、侧视 图、俯视图均为等腰直角三角形,且直角边长都为1,则它的外接球的表面积是( )| A. | 3π | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com