Question

8．已知△ABC中，$|{\overrightarrow{BC}}|=8，\overrightarrow{AB}•\overrightarrow{AC}=-9$，D为边BC的中点，则$|{\overrightarrow{AD}}|$=$\sqrt{7}$．

Answer 1

分析 利用数量积的性质和向量的平行四边形法则即可得出．

解答 解：如图，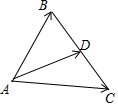

$|\overrightarrow{BC}{|}^{2}=（\overrightarrow{BC}）^{2}=（\overrightarrow{AC}-\overrightarrow{AB}）^{2}$=$|\overrightarrow{AC}{|}^{2}-2\overrightarrow{AC}•\overrightarrow{AB}+|\overrightarrow{AB}{|}^{2}=64$，
∴$\overrightarrow{AC}{|}^{2}+|\overrightarrow{BC}{|}^{2}=46$$|\overrightarrow{AC}{|}^{2}+|\overrightarrow{BC}{|}^{2}=46$．
∴$|\overrightarrow{AD}{|}^{2}=\frac{1}{4}（\overrightarrow{AB}+\overrightarrow{AC}）^{2}$=$\frac{1}{4}（|\overrightarrow{AB}{|}^{2}+|\overrightarrow{AC}{|}^{2}+2\overrightarrow{AB}•\overrightarrow{AC}）$=$\frac{1}{4}（46-18）=7$．
∴$|{\overrightarrow{AD}}|$=$\sqrt{7}$．
故答案为：$\sqrt{7}$．

点评 本题考查了数量积的性质和向量的平行四边形法则，属于中档题．