Question

在正棱锥P-ABC中，三条側棱两两互相垂直，G是△PAB的重心，E，F分别为BC，PB上的点，且BE：EC=PF：FB=1：2．
（1）求证：平面GEF⊥平面PBC；
（2）求证：EG是PG与BC的公垂线段．

Answer 1

【答案】分析：（1）根据PA、PB、PC两两垂直，则PA⊥平面PBC，而根据重心的性质可知GF∥PA，最后根据平行线的性质可得GF⊥平面PBC，进而由面面垂直的判定定理得到平面GEF⊥平面PBC；
（2）取EC的中点H，连接FH，利用平行线分线段成比例定理可得FH∥PC，进而可得FB=FH，进而由等腰三角形三线合一，可得EF⊥BC，结合（1）的结论及线面垂直的判定及性质定理，可得PG⊥GN，取FB的中点N，利用平行线分线段成比例定理可得GN∥BD，由等腰三角形PAB中，BD⊥PD，可得PG⊥GN，再平行线分线段成比例定理可得NE∥PC，进而根据已知判断出PC⊥平面PAB，进而PC⊥PG，NE⊥PG，结合线面垂直的判定及性质得到PG⊥EG，综合后可得EG是PG与BC的公垂线段
解答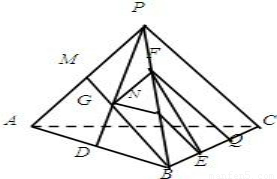：证明：（1）在△PAB中，∵G是△PAB的重心，
∴MG=MB，
∵PF：FB=1：2，即PF=PB，
∴GF∥PM
又PA、PB、PC两两垂直，
∴PA⊥平面PBC，又∵GF∥PA
∴GF⊥平面PBC
又∵GF?平面GEF
∴平面GEF⊥平面PBC；
（2）取EC的中点Q，连接FQ，
∵BE：EC=PF：FB=1：2
∴BQ：QC=2：1
∴FQ∥PC
∴FB=FQ
∴EF⊥BC
又∵GF⊥平面PBC
∴GF⊥BC
由GF∩EF=F
∴BC⊥平面GEF
∴EG⊥BC
取FB的中点N，则PG：GD=PN：NB=2：1
即GN∥BD
在等腰三角形PAB中，BD⊥PD
∴PG⊥GN
又∵PN：NB=CE：EB=2：1
∴NE∥PC
由又PA、PB、PC两两垂直，
∴PC⊥平面PAB，
又∵PG?平面PAB
∴PC⊥PG
∴NE⊥PG
又NE∩GN=N
∴PG⊥平面GNE
∴PG⊥EG
即EG是PG与BC的公垂线段
点评：本题主要考查了直线与平面垂直的判定，以及直线与平面平行的判定，同时考查了推理论证的能力，属于中档题．