解:(Ⅰ)f(x)=

+3=(2cosωx,-1)•(sinωx-cosωx,2)+3 …(1分)
=2cosωx(sinωx-cosωx)+1 …(2分)
=2sinωxcosωx-2cos
2ωx+1 …(3分)
=sin2ωx-cos2ωx …(4分)
=

sin
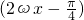
. …(5分)
∵T=π,且ω>0,∴ω=1.…(6分)
(Ⅱ) 由(Ⅰ)知:f(x)=

sin
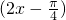
,…(7分)
y=Asin(ωx+∅)的图象变换规律可得 g(x)=

•

sin
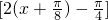
=2sin2x. …(9分)
由2kπ-

≤2x≤2kπ+

,k∈Z;…(10分)
解得kπ-

≤x≤kπ+

,k∈Z;…(11分)
∴函数g(x)的单调增区间为
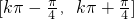
,k∈Z.…(12分)
分析:(Ⅰ)利用三角函数的恒等变换化简f(x)的解析式为

sin
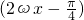
,根据周期求出ω的值.
(Ⅱ) 由(Ⅰ)知:f(x)=

sin
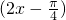
,再根据y=Asin(ωx+∅)的图象变换规律可得 g(x)=

•

sin
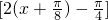
=2sin2x,由2kπ-

≤2x≤2kπ+

,k∈Z,求得x的范围,即可得到函数g(x)的单调增区间.
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的单调增区间,y=Asin(ωx+∅)的图象变换规律,属于中档题.

 =(2cosωx,-1),
=(2cosωx,-1), =(sinωx-cosωx,2),函数f(x)=
=(sinωx-cosωx,2),函数f(x)= •
• +3的周期为π.
+3的周期为π. ,再横坐标不变,纵坐标伸长到原来的
,再横坐标不变,纵坐标伸长到原来的 倍,得到函数g(x)的图象,求函数g(x)的单调增区间.
倍,得到函数g(x)的图象,求函数g(x)的单调增区间. +3=(2cosωx,-1)•(sinωx-cosωx,2)+3 …(1分)
+3=(2cosωx,-1)•(sinωx-cosωx,2)+3 …(1分) sin
sin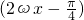 . …(5分)
. …(5分) sin
sin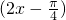 ,…(7分)
,…(7分) •
• sin
sin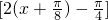 =2sin2x. …(9分)
=2sin2x. …(9分) ≤2x≤2kπ+
≤2x≤2kπ+ ,k∈Z;…(10分)
,k∈Z;…(10分) ≤x≤kπ+
≤x≤kπ+ ,k∈Z;…(11分)
,k∈Z;…(11分)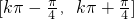 ,k∈Z.…(12分)
,k∈Z.…(12分) sin
sin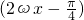 ,根据周期求出ω的值.
,根据周期求出ω的值.  sin
sin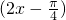 ,再根据y=Asin(ωx+∅)的图象变换规律可得 g(x)=
,再根据y=Asin(ωx+∅)的图象变换规律可得 g(x)= •
• sin
sin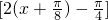 =2sin2x,由2kπ-
=2sin2x,由2kπ- ≤2x≤2kπ+
≤2x≤2kπ+ ,k∈Z,求得x的范围,即可得到函数g(x)的单调增区间.
,k∈Z,求得x的范围,即可得到函数g(x)的单调增区间.
