
规定![]() =
=![]() ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且![]() ,这是组合数
,这是组合数![]() (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.
(1)求![]() 的值.
的值.
(2)设x>0,当x为何值时,![]() 取最小值?
取最小值?
(3)我们知道组合数具有如下两个性质:
①![]() =
=![]() ;②
;②![]() +
+![]() =
=![]() .
.
是否都能推广到![]() (x∈R,m是正整数)的情形?若能推广,请写出推广的形式,并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,请写出推广的形式,并给出证明;若不能,则说明理由.
(4)已知组合数![]() 是正整数,证明当x∈Z,m是正整数时,
是正整数,证明当x∈Z,m是正整数时,![]() ∈Z.
∈Z.
思路解析:本题是有关组合数知识的延伸,着重考查考生接受新知识的能力.在解决过程中,要注意充分利用题目中的Cmx的定义以及结合所学的相关知识,从而将问题解决.
解:(1)![]() =
=![]() =-680.
=-680.
(2)![]() =
=![]() =
=![]() (x+
(x+![]() -3),
-3),
∵x>0,x+![]() ≥2
≥2![]() ,当且仅当x=
,当且仅当x=![]() 时,等号成立.∴当x=
时,等号成立.∴当x=![]() 时,
时,![]() 取得最小值.
取得最小值.
(3)性质①不能推广.例如当x=![]() 时,
时,![]() 有意义,但
有意义,但![]() 无意义;性质②能推广,它的推广形式是
无意义;性质②能推广,它的推广形式是![]() +
+![]() =
=![]() ,x∈R,m是正整数,事实上
,x∈R,m是正整数,事实上
当m=1时,有![]() +
+![]() =x+1=
=x+1=![]() ,当m≥2时,
,当m≥2时,
Cmx+Cm-1x=![]() +
+![]() =
=
![]() (
(![]() +1)=
+1)=![]() =
= ![]() ,
,
(4)证明:当x≥m时,组合数![]() ∈Z.
∈Z.
当0≤x<m时,![]() =0∈Z,当x<0时,∵-x+m+1>0,
=0∈Z,当x<0时,∵-x+m+1>0,
∴![]() =
=![]() =(-1)m
=(-1)m![]()
![]() ,∈Z.
,∈Z.


科目:高中数学 来源: 题型:
| C | m x |
| x(x-1)…(x-m+1) |
| m! |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OP |
| 16 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| C | m x |
| x(x-1)…(x-m+1) |
| m! |
| C | 0 x |
| C | m n |
| C | 3 -15 |
| ||
(
|
| C | m n |
| C | n-m n |
| C | m n |
| C | m-1 n |
| C | m n+1 |
| C | m x |
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
规定![]() =
=![]() ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且![]() =1,这是组合数
=1,这是组合数![]() (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.
(1)求![]() 的值;
的值;
(2)组合数的两个性质:
①![]() =
=![]() ;②
;②![]() +
+![]() =
=![]() .
.
是否都能推广到![]() (x∈R,m是正整数)的情形?若能推广,写出推广的形式并给出证明;若不能推广,则说明理由;
(x∈R,m是正整数)的情形?若能推广,写出推广的形式并给出证明;若不能推广,则说明理由;
(3)已知组合数![]() 是正整数,证明:当x∈Z,m是正整数时,
是正整数,证明:当x∈Z,m是正整数时,![]() ∈Z.
∈Z.
查看答案和解析>>
科目:高中数学 来源:2011年云南省高三数学一轮复习章节练习:计数原理(解析版) 题型:解答题
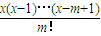 ,其中x∈R,m是正整数,且Cx=1,这是组合数Cmn(n、m是正整数,且m≤n)的一种推广.
,其中x∈R,m是正整数,且Cx=1,这是组合数Cmn(n、m是正整数,且m≤n)的一种推广.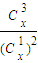 取得最小值?
取得最小值?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com