
规定![]() =
=![]() ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且![]() =1,这是组合数
=1,这是组合数![]() (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.
(1)求![]() 的值;
的值;
(2)组合数的两个性质:
①![]() =
=![]() ;②
;②![]() +
+![]() =
=![]() .
.
是否都能推广到![]() (x∈R,m是正整数)的情形?若能推广,写出推广的形式并给出证明;若不能推广,则说明理由;
(x∈R,m是正整数)的情形?若能推广,写出推广的形式并给出证明;若不能推广,则说明理由;
(3)已知组合数![]() 是正整数,证明:当x∈Z,m是正整数时,
是正整数,证明:当x∈Z,m是正整数时,![]() ∈Z.
∈Z.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2008-2009学年度山东省莱阳一中第一学期高三数学学段检测(文) 题型:044
对定义域是Df,Dg的函数y=f(x),y=g(x),规定: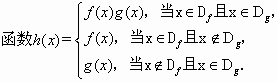
(Ⅰ)若函数f(x)=![]() ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式;
(Ⅱ)求问题(1)中函数h(x)的值域;
(Ⅲ)若g(x)=f(x+α),其中α是常数,且α∈[0,π],请设计一个定义域为R的函数,y=f(x),及一个α的值,使得h(x)=cos4x,并予以证明.
查看答案和解析>>
科目:高中数学 来源:山东省蓬莱、牟平2006—2007学年度第一学期高三年级期中考试、数学试题(文科) 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
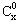 =1,这是组合数
=1,这是组合数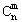 (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.
(1)求C![]() 的值;
的值;
(2)组合数的两个性质;
①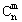 =C
=C![]() . ②
. ②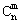 +C
+C![]() =C
=C![]() .
.
是否都能推广到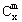 (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(3)已知组知数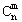 是正整数,证明:当x∈Z,m是正整数时,
是正整数,证明:当x∈Z,m是正整数时,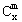 ∈Z
∈Z
查看答案和解析>>
科目:高中数学 来源: 题型:
22.规定C![]() =
=![]() ,其中x∈R,m是正整数,且 C
,其中x∈R,m是正整数,且 C![]() =1,
=1,
这是组合数C![]() (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.
(1)求C![]() 的值;
的值;
(2)设x>0中,当x为何值时,![]() 取得最小值?
取得最小值?
(3)组合数的两个性质;
①C![]() =C
=C![]() . ②C
. ②C![]() +C
+C![]() =C
=C![]() .
.
是否都能推广到C![]() (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com