
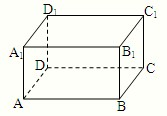
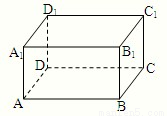
 如图,以长方体ABCD-A1B1C1D1的顶点A、C及另两个顶点为顶点构造四面体.
如图,以长方体ABCD-A1B1C1D1的顶点A、C及另两个顶点为顶点构造四面体.abc-4×
| ||
| abc |
| 1 |
| 3 |


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
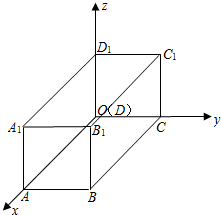 如图,以长方体ABCD-A1B1C1D1的一个顶点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.已知点B1的坐标是(2,1,1).
如图,以长方体ABCD-A1B1C1D1的一个顶点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.已知点B1的坐标是(2,1,1).| AD1 |
| A1C1 |
| BA1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
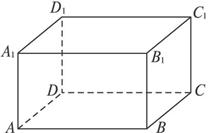
(1)若该四面体的四个面都是直角三角形,试写出一个这样的四面体(不要求证明);
(2)我们将四面体中两条无公共端点的棱叫做对棱,若该四面体的任一对对棱垂直,试写出一个这样的四面体(不要求证明);
(3)若该四面体的任一对对棱相等,试写出一个这样的四面体(不要求证明),并计算它的体积与长方体的体积的比.
查看答案和解析>>
科目:高中数学 来源: 题型:
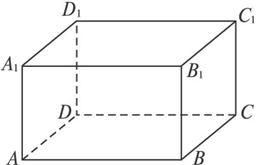
(1)若该四面体的四个面都是直角三角形,试写出一个这样的四面体(不要求证明);
(2)我们将四面体中两条无公共端点的棱叫做对棱,若该四面体的任一对对棱垂直,试写出一个这样的四面体(不要求证明);
(3)若该四面体的任一对对棱相等,试写出一个这样的四面体(不要求证明),并计算它的体积与长方体的体积的比.
查看答案和解析>>
科目:高中数学 来源:2009年江苏省南京市金陵中学高考数学三模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com